Sommaire
Le dimensionnement d’un réseau de ventilation consiste à calculer le diamètre de chaque conduit et d’en déduire la hauteur manométrique à fournir par le ventilateur.
Exemple de base
Les différentes méthodes de dimensionnement seront appliquées ci-après à l’exemple de réseau de distribution suivant :
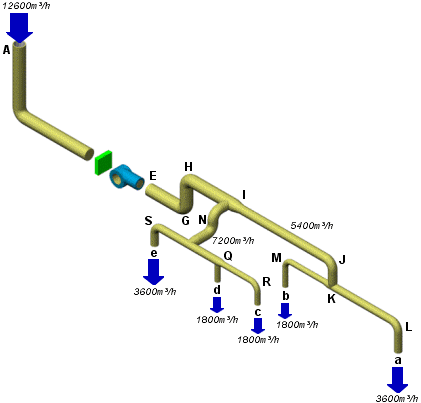
Le débit à fournir par le ventilateur est de 12 600 m³/h. Il se répartit en 5 bouches de pulsion :
| Bouche | Débit pulsé |
| Bouche a | 3 600 [m³/h] |
| Bouche b | 1 800 [m³/h] |
| Bouche c | 1 800 [m³/h] |
| Bouche d | 3 600 [m³/h] |
| Bouche e | 1 800 [m³/h] |
Pour pulser le débit souhaité, les bouches doivent être alimentées sous une pression de 50 Pa.
Méthode des pertes de charge constantes par branche
Cette méthode consiste à fixer la perte de charge linéaire dans la branche du réseau la plus résistante (a priori, la plus longue), par exemple à une valeur de 1 Pa/m (valeur courante de compromis entre les problèmes acoustiques liés à une vitesse trop élevée de l’air et l’investissement lié à la taille des conduits). Ensuite, en partant de la bouche la plus défavorisée, on égalise la perte de charge de chacune des branches parallèles, ce qui permet d’en déterminer le diamètre. On obtient ainsi en final un réseau directement équilibré.
Suivant des tables reprises dans la littérature, les accidents de parcours (coudes, changements de section, tés, bifurcations, …) sont assimilés à une longueur de conduite équivalente, c’est-à-dire ayant la même perte de charge.
En reprenant l’exemple de base :
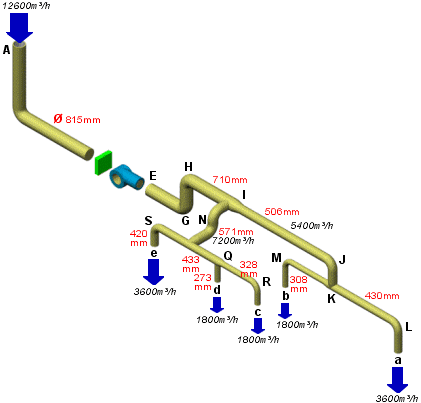
Tronçon E-a
On fixe dans ce tronçon la perte de charge linéaire à 1 Pa/m. Connaissant la longueur des conduits et la longueur équivalente des accidents, on déduit immédiatement la perte de charge du tronçon. Ensuite, connaissant la perte de charge linéaire et le débit véhiculé par un tronçon, on peut immédiatement calculer sa section en fonction du débit, en se référant aux abaques couramment rencontrés dans la littérature (fonction de la forme du conduit et de sa composition).
L’exemple est ici donné pour des conduits circulaires. Il est semblable pour des conduites rectangulaires.
|
Tronçon |
Débit |
q |
Longueur |
Dp lin |
Dp |
Σ Dp |
Diam |
Vitesse |
| – |
[m³/h] |
[m³/s] |
[m] |
[Pa/m] |
[Pa] |
[Pa] |
[mm] |
[m/s] |
| E-F | 12 600 | 3,5 | 1 | 1 | 1 | 1 | – | – |
| F-G | 12 600 | 3,5 | 2 | 1 | 2 | 3 | 710 | 8,85 |
| G | 12 600 | 3,5 | 7 | 1 | 7 | 10 | 710 | 8,85 |
| G-H | 12 600 | 3,5 | 3 | 1 | 3 | 13 | 710 | 8,85 |
| H | 12 600 | 3,5 | 7 | 1 | 7 | 20 | 710 | 8,85 |
| H-I | 12 600 | 3,5 | 4 | 1 | 4 | 24 | 710 | 8,85 |
| I | 12 600 | 3,5 | 7 | 1 | 7 | 31 | 710 | 8,85 |
| I-J | 5 400 | 1,5 | 8 | 1 | 8 | 39 | 506 | 7,47 |
| J | 5 400 | 1,5 | 5 | 1 | 5 | 44 | 506 | 7,47 |
| J-K | 5 400 | 1,5 | 1 | 1 | 1 | 45 | 506 | 7,47 |
| K | 5 400 | 1,5 | 5 | 1 | 5 | 50 | 506 | 7,47 |
| K-L | 3 600 | 1 | 9 | 1 | 9 | 59 | 430 | 6,89 |
| L | 3 600 | 1 | 4 | 1 | 4 | 63 | 430 | 6,89 |
| L-a | 3 600 | 1 | 2 | 1 | 2 | 65 | 430 | 6,89 |
| a | 3 600 | 1 | – | – | (50) | 115 | – | – |
Tronçon K-b
En E, la pression est de 115 Pa. En K, elle est de 115 – 45 = 70 Pa.
Pour que le réseau soit équilibré, la perte de charge du tronçon K-b doit être identique à la perte de charge du tronçon K-a, à savoir 70 – 50 = 20 Pa
La longueur du tronçon K-b est de 9 m, à laquelle vient s’ajouter la longueur équivalente du coude (6 m), ce qui donne une longueur de 15 m pour une perte de charge de 20 Pa, soit une perte de charge linéaire de 1,33 Pa
On en déduit comme pour le tronçon précédent le diamètre des conduits en fonction du débit véhiculé.
|
Tronçon |
Débit |
q |
Longueur |
Dp lin |
Dp |
Σ Dp |
Diam |
Vitesse |
| – |
[m³/h] |
[m³/s] |
[m] |
[Pa/m] |
[Pa] |
[Pa] |
[mm] |
[m/s] |
| K-M | 1 800 | 0,5 | 7 | 1,33 | 9 | 9 | 308 | 6,73 |
| M | 1 800 | 0,5 | 6 | 1,33 | 8 | 17 | 308 | 6,73 |
| M-b | 1 800 | 0,5 | 2 | 1,33 | 3 | 20 | 308 | 6,73 |
| b | 1 800 | 0,5 | – | – | (50) | 70 | – | – |
Tronçon I-c
En I, la pression est de 115 – 31 = 84 Pa.
Pour que le réseau soit équilibré, la perte de charge du tronçon I-c doit être identique à la perte de charge du tronçon K-a, à savoir 84 – 50 = 34 Pa.
Le tronçon I-c comporte 13 m de section droite et 25 m de longueur équivalente due aux coudes et changement de section, ce qui donne une longueur de 38 m pour une perte de charge de 34 Pa, soit une perte de charge linéaire de 0,97 Pa On en déduit comme pour les tronçons précédents le diamètre des conduits en fonction du débit.
|
Tronçon |
Débit |
q |
Longueur |
Dp lin |
Dp |
Σ Dp |
Diam |
Vitesse |
| – |
[m³/h] |
[m³/s] |
[m] |
[Pa/m] |
[Pa] |
[Pa] |
[mm] |
[m/s] |
| I-N | 7 200 | 2 | 2 | 0,97 | 2 | 2 | 571 | 7,82 |
| N | 7 200 | 2 | 6 | 0,97 | 6 | 8 | 571 | 7,82 |
| N-O | 7 200 | 2 | 1 | 0,97 | 1 | 9 | 571 | 7,82 |
| O | 7 200 | 2 | 6 | 0,97 | 6 | 15 | 571 | 7,82 |
| O-P | 7 200 | 2 | 3 | 0,97 | 3 | 17 | 571 | 7,82 |
| P | 7 200 | 2 | 4 | 0,97 | 4 | 21 | 571 | 7,82 |
| P-Q | 3 600 | 1 | 3 | 0,97 | 3 | 24 | 433 | 6,81 |
| Q | 1 800 | 0,5 | 3 | 0,97 | 3 | 27 | 328 | 5,93 |
| Q-R | 1 800 | 0,5 | 3 | 0,97 | 3 | 30 | 328 | 5,93 |
| R | 1 800 | 0,5 | 3 | 0,97 | 3 | 33 | 328 | 5,93 |
| R-c | 1 800 | 0,5 | 1 | 0,97 | 1 | 34 | 328 | 5,93 |
| c | 1 800 | 0,5 | – | – | (50) | 84 | – | – |
Tronçon P-e
En P, la pression est de 84 – 22 = 62 Pa.
Pour que le réseau soit équilibré, la perte de charge du tronçon PE doit être identique à la perte de charge du tronçon P-c, à savoir 62 – 50 = 12 Pa.
Le tronçon PE comporte 6 m de section droite et 4 m de longueur équivalente due au coude, ce qui donne une longueur de 10 m pour une perte de charge de 12 Pa. La perte de charge linéaire est donc de 1,26 Pa.
|
Tronçon |
Débit |
q |
Longueur |
Dp lin |
Dp |
Σ Dp |
Diam |
Vitesse |
| – |
[m³/h] |
[m³/s] |
[m] |
[Pa/m] |
[Pa] |
[Pa] |
[mm] |
[m/s] |
| P-S | 3 600 | 1 | 5 | 1,26 | 6 | 6 | 410 | 7,56 |
| S | 3 600 | 1 | 4 | 1,26 | 5 | 11 | 410 | 7,56 |
| S-e | 3 600 | 1 | 1 | 1,26 | 1 | 13 | 410 | 7,56 |
| e | 3 600 | 1 | – | – | 50 | 63 | – | – |
Tronçon Q-d
En Q, la perte de charge du tronçon Q-d doit être identique à la perte de charge du tronçon Q-c, à savoir 10 PA Le tronçon PE comporte 1 m de section droite et 3 m de longueur équivalente due au piquage, ce qui donne une longueur de 4 m pour une perte de charge de 10 Pa, soit une perte de charge linéaire de 2,43 Pa.
|
Tronçon |
Débit |
q |
Longueur |
Dp lin |
Dp |
Σ Dp |
Diam |
Vitesse |
| – |
[m³/h] |
[m³/s] |
[m] |
[Pa/m] |
[Pa] |
[Pa] |
[mm] |
[m/s] |
| Q | 1 800 | 0,5 | 3 | 2,43 | 7 | 7 | 273 | 8,55 |
| Q-d | 1 800 | 0,5 | 1 | 2,43 | 2 | 10 | 273 | 8,55 |
| d | 1 800 | 0,5 | – | – | 50 | 60 | – | – |
Tronçon A-E
La pression nécessaire au niveau de la prise d’air extérieure est de 40 Pa La perte de charge du filtre est de 45 Pa (modification de section comprise). On se fixe dans ce premier tronçon une perte de charge de 0,5 Pa/m.
|
Tronçon |
Débit |
q |
Longueur |
Dp lin |
Dp |
Σ Dp |
Diam |
Vitesse |
| – |
[m³/h] |
[m³/s] |
[m] |
[Pa/m] |
[Pa] |
[Pa] |
[mm] |
[m/s] |
| A | 12 600 | 3,5 | – | – | (40) | 40 | – | – |
| A-B | 12 600 | 3,5 | 4 | 0,5 | 2 | 42 | 815 | 6,70 |
| B | 12 600 | 3,5 | 8 | 0,5 | 4 | 46 | 815 | 6,70 |
| B-C | 12 600 | 3,5 | 2 | 0,5 | 1 | 47 | 815 | 6,70 |
| C-D | 12 600 | 3,5 | – | – | (45) | 92 | – | – |
| D-E | 12 600 | 3,5 | – | – | (0,5) | 92,5 | – | – |
Dimensionnement du ventilateur
Le ventilateur doit donc fournir un débit de 12 600 m³/h, avec une pression de 115 + 92,5 = 207,5 Pa
Méthode de la vitesse constante dans la branche la plus résistante
Plutôt que de se fixer une perte de charge linéaire constante dans le tronçon le plus défavorisé (E-a), on peut y fixer une vitesse (exemple : 6,5 m/s).
Puisque l’on connaît la vitesse dans ce tronçon, on peut calculer automatiquement les sections et les diamètres des conduits en fonction du débit véhiculé puisque :
Section = Débit / Vitesse
La perte de charge de chaque section est alors déterminée par des abaques en fonction du type de conduit choisi.
Une fois que l’on a déterminé les sections du premier tronçon, les sections et les pertes de charge de chaque tronçon sont calculées comme dans la méthode précédente.
Méthode des pertes de charge linéaires ou des vitesses dans toutes les branches
Pour simplifier le calcul, on peut également fixer soit la perte de charge linéaire, soit la vitesse dans l’entièreté du réseau de distribution. Les bouches sont alors choisies en fonction de la pression disponible en amont. Si cette pression est trop importante, il faudra diminuer la section du conduit du tronçon ou installer un registre de réglage. Cette méthode est plus simple mais demande quand même le calcul des pressions disponibles à chaque bouche. Leur choix et leur ajustement sont en outre plus complexes.
Outils informatiques
La complexité des réseaux peut rendre fastidieux le calcul d’un réseau complet, surtout si on veut multiplier les essais de manière à optimaliser la solution, en terme d’investissement, de consommation énergétique, de bruit, ….
Heureusement, il existe sur le marché des programmes informatiques qui intègrent les différentes méthodes de calcul et qui fournissent également comme résultats, les surfaces de réseau, son poids, les déperditions en fonction de la température du fluide transporté, des vitesses d’air et des matériaux.
Projet OPTIVENT
Pour les installations résidentielles, le CSTC a développé récemment lors du projet OPTIVENT un outil de calcul informatique gratuit permettent de concevoir, dimensionner et équilibrer un réseau de ventilation.
![Connaître les paramètres principaux [ventilation]](https://energieplus-lesite.be/wp-content/uploads/2007/09/dimensionnementPetit-500x383.gif)
Auteur : les anciens
Notes :
[…] entre les deux côtés de la grille. Cela est dû aux frottements de l’air en mouvement11. Si elle est trop élevée, les équipements de ventilation ne pourront pas fonctionner […]