Sommaire

La pression partielle de vapeur
L’air que nous respirons contient toujours un peu de vapeur d’eau. On peut considérer cette vapeur comme un gaz, dont la pression fait partie de la pression atmosphérique. La pression de la vapeur d’eau, à elle seule, est dénommée pression partielle de vapeur d’eau, et est représentée par le symbole pv. Ainsi, la vapeur d’eau contenue dans un air à 20°C et 50 % HR présente une pression de vapeur partielle de 1 170 Pa (par comparaison, la pression atmosphérique est de 101 300 PA).
Si la pression de la vapeur d’eau atteint sa valeur maximale, il y a saturation de l’air et on parle de pression partielle de la vapeur d’eau à la saturation, ou de pression saturante pvs.
Il est possible de calculer la valeur de la pression de saturation en fonction de la température.
L’humidité absolue
L’humidité absolue [geau/kgair sec] représente le nombre de grammes de vapeur d’eau présents dans un volume donné, rapporté à la masse d’air sec de ce volume exprimé en kilogramme.
Dans le système d’unités SI, on utilisera le kgeau/kgair sec. Comme symbole, les lettres “x”, ou “w”, ou “r” sont généralement utilisées.
Puisque 1 m³ d’air pèse environ 1,2 kg, en ajoutant 20 % à la valeur de l’humidité absolue, on obtient la quantité d’eau présente par m³ d’air.
Exemple : de l’air à 20°C, 50 % HR, contient 7,36 grammes d’eau par kg, soit 8,7 grammes d’eau par m³.
Nous donnons ci-dessous quelques valeurs indicatives :
| Température [°C] |
Humidité absolue en [geau/kgair sec] |
||
| A | à l’extérieur en hiver (HR = 80 %) |
-5 | 2,1 |
| B | dans un local (HR = 60 %) |
18 | 7,8 |
| C | dans un local (HR = 60 %) |
20 | 8,8 |
| D | à l’extérieur en été (HR = 70 %) |
25 | 14 |
Ces valeurs d’humidité absolue sont lues sur les ordonnées d’un diagramme de l’air humide.
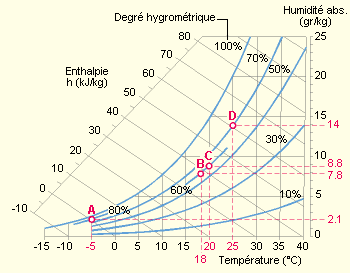
On voit donc que, pour des climats “standards”, plus la température augmente et plus l’humidité absolue est élevée (plus l’air peut porter de l’eau à l’état vapeur).
Dans nos régions, on peut dire qu’en hiver l’air est “sec”, même s’il pleut dehors (parce que l’humidité absolue est faible), et qu’en été, l’air est “humide” même s’il y a du soleil (parce que l’humidité absolue contenue par m³ d’air est élevée).
Il est possible de calculer l’humidité absolue en fonction de la pression partielle.
L’humidité relative
L’humidité relative s’exprime en %.
C’est le rapport entre la pression partielle de vapeur d’eau “pv” et la pression de saturation de la vapeur d’eau “pvs“. Le symbole représentatif est souvent .
φ = 100 . pv / pvs
En bonne approximation, sa valeur est proche du rapport entre l’humidité absolue portée par l’air et l’humidité absolue maximale qu’il peut porter lorsqu’il est saturé. Ceci donne une signification intuitive à cette grandeur : pour une température donnée, elle caractérise en somme la faculté que possède l’air d’absorber encore de la vapeur d’eau avant qu’elle ne condense. Par exemple, 40 % d’humidité relative signifie que l’air peut absorber encore beaucoup de vapeur d’eau puisqu’il n’est qu’à 40 % de la saturation. A 100 %, on est à la limite de la saturation de l’air par la vapeur d’eau, du brouillard apparaît.
Ci-dessous, quelques valeurs d’humidité relative obtenues en chauffant l’air extérieur qui pénètre dans un bâtiment par les joints de fenêtres ou les ouvertures.
| Température [°C] | Humidité absolue [geau/kgairsec] | Humidité relative [%] |
Remarques | ||
| A | automne (matin) |
6,5 | 6 | 100 | brouillard ou pluie |
| B | automne | 10 | 6 | 79 | brouillard ou brume |
| C | chauffé à | 15 | 6 | 57 | |
| D | chauffé à | 18 | 6 | 47 | |
| E | chauffé à | 20 | 6 | 41 |
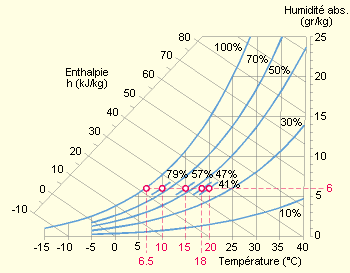
Du point de vue climatique, la pression de vapeur et l’humidité relative de l’air extérieur varient durant la journée et durant l’année. Ainsi, au cours des variations de température d’une journée, la pression de vapeur (pe) varie peu, mais l’humidité relative (φe) varie fortement. Par contre, au cours des variations de température d’une année (de mois en mois), c’est le contraire : la pression de vapeur moyenne varie fortement, mais l’humidité relative moyenne varie peu.
| J | F | M | A | M | J | J | A | S | O | N | D | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| φe (%) |
91
|
87
|
85
|
81
|
77
|
80
|
79
|
83
|
83
|
91
|
91
|
91
|
| Pe (N/m²) |
730
|
668
|
857
|
935 |
1072
|
1520
|
1445
|
1618
|
1352
|
1194
|
856
|
694
|
|
Pression de vapeur et humidité relative moyenne mensuelle. |
||||||||||||
Cette différence s’explique par la lenteur de l’évaporation de l’eau. En effet, une hausse de température au cours d’une journée ne suffit pas à évaporer l’eau. La pression de vapeur reste donc identique. Or, l’air pourrait contenir plus d’eau. Par conséquent, l’humidité relative diminue. Ainsi une augmentation de température peut entraîner des humidités relatives momentanément très basses.
Par contre, avec une hausse de température plus longue (à l’échelle du mois), l’évaporation a le temps de se produire. Par conséquent, la pression de vapeur augmente. L’humidité relative reste, quant à elle, constante.
Néanmoins, lors de précipitations, l’eau se présente sous forme optimale pour s’évaporer facilement (principe du vaporisateur). L’humidité relative augmente rapidement jusqu’à 100 % indépendamment de la température.
Ensuite, si la température baisse, le point de rosée de l’air peut être atteint, du brouillard se forme.
De même, dans une région boisée ou alluviale, l’air sera toujours plus humide que dans un site urbanisé (microclimats différents).
L’enthalpie spécifique
L’enthalpie spécifique représente la quantité de chaleur contenue dans l’air humide dont la masse d’air sec est de 1 kg. C’est donc la somme de la chaleur sensible (liée à la température de l’air) et de la chaleur latente (liée à l’énergie de la vapeur d’eau qu’il contient).
Par convention, on a fixé l’enthalpie de l’air sec à 0°C comme étant zéro. De l’air à – 10°C peut donc avoir une enthalpie négative.
Le symbole représentatif est généralement h. Il s’exprime en kJ/kgair sec.
h = enthalpie de l’air sec + enthalpie de la vapeur, soit approximativement :
h = 1,006 . η+ x . (2 501 + 1,83 . η ) [kJ/kg air sec]
où, x est l’humidité absolue et η la température
L’enthalpie contenue dans l’air peut également être lue sur le diagramme de l’air humide.
Exemple :
Soit η= 25°C et x = 0,008 kgeau/kgair,
alors h = 1,006 . 25 + 0,008 . (2 501 + 1,83 . 25) = 45,5 kJ/kg air sec
Le volume spécifique et la masse volumique
Le volume spécifique représente le volume occupé par l’air humide dont la masse d’air sec est de 1 kg. Son symbole est généralement “v”.
Exemple.
un air de 20°C et 50 % HR présente un volume spécifique de 0,84 m³/kgair sec.
La masse volumique représente la masse d’air sec occupé par 1 m³ d’air humide. Son symbole est généralement “ρ”.
Exemple.
un air de 20°C et 50 % HR présente une masse volumique de 1,18 kgair sec/m³
Il est possible de calculer ces valeurs.
La température de rosée
Imaginons de l’air qui serait refroidi, tout en gardant son humidité absolue constante. Cet air va perdre de plus en plus la faculté de porter de l’eau à l’état vapeur. Au moment où tout l’air sera saturé, et que diminuer encore la température engendrerait la condensation partielle de la vapeur d’eau, on sait que l’on a atteint la température de rosée de l’air. Son symbole est ηr ou tr.
Sur le diagramme de l’air humide, la température de rosée d’une ambiance correspond à l’intersection entre l’horizontale du point d’ambiance et la courbe de saturation.
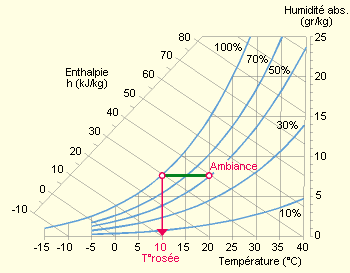
Il est possible de calculer cette valeur en fonction de la pression partielle de vapeur.
La température “bulbe humide”
La température bulbe humide ou température humide est la température indiquée par un thermomètre dit “à bulbe humide”, ou psychromètre. Avant l’arrivée des appareils de mesure électroniques, il permettait de mesurer le taux d’humidité d’un local. Le procédé est le suivant :
Deux thermomètres sont soumis à un flux d’air forcé. Le premier indique la température de l’air de l’ambiance. Le deuxième est entouré d’ouate humide. L’air qui entre dans l’ouate s’humidifie. Il se refroidit également puisque l’eau s’évapore et prélève la chaleur de vaporisation nécessaire dans l’air.
En bonne approximation, sur le diagramme de l’air humide, l’air suit une isenthalpique et atteint la saturation. Connaissant la température à la saturation et la température normale, on peut déduire le taux d’humidité relative de l’air sur le diagramme.
Le symbole de la température humide est ηh ou th.
Il est possible également de calculer cette valeur.
Les relations entre grandeurs hygrométriques
Il est souvent plus rapide de consulter un abaque ou le diagramme de l’air humide, mais les relations mathématiques reprises ci-dessous entre les grandeurs peuvent être utiles notamment lors d’une automatisation de la régulation, avec programmation entre ces variables.
Entre la pression de vapeur saturante et la température η , en présence d’eau liquide (η> 0°C)
pvs = 102,7877 + (7,625 . η ) / (241,6 + η )
| Exemple.
A 25°, la pression de vapeur saturante est de : pvs = 102,7877 + (7,625 . 25) / (241,6 + 25) = 3 182 PA, (contre 3 167 en réalité) |
Entre la pression de vapeur saturante et la température η , en présence de glace (η < 0°C)
pvs = 102,7877 + (9,756 . η ) / (272,7 + η)
Entre l’humidité absolue et la pression partielle de vapeur d’eau
L’humidité absolue “²w” est liée à la pression partielle de vapeur d’eau “pv” par la relation :
x = 0,622 . (pv / (Patm – pv))
où,
- x est exprimé en kg eau/kg air sec
- pv est la pression partielle de vapeur d’eau
- P est pression totale de l’air humide, que l’on peut en première approche prendre égale à la pression atmosphérique, soit 101 300 Pa
| Exemple.
A 29°C et une pression partielle de vapeur de 2 000 Pa, on obtient : x = 0,622 . (2 000 / (101 300 – 2 000)) = 0,0125 kg eau/kg air sec, soit 12,5 g eau/kg air sec. |
Entre l’enthalpie, la température et l’humidité absolue
h = 1,006 . η + x . (2 501 + 1,83 . η ) en kJ/kg air sec
où,
- x est l’humidité absolue et η la température
| Exemple.
soit η = 25°C et x = 0,008 kgeau/kgair sec, alors h = 1,006 . 25 + 0,008 . (2 501 + 1,83 . 25) = 45,5 kJ/kg air sec |
Entre l’enthalpie, la température et l’humidité relative
h = 1,006 . η+ [0,622 . (pv / (Patm – pv))] . (2 501 + 1,83 . η) en kJ/kg air sec
avec pv = φ . pvs =φ . 102,7877 + (7,625 . η ) / (241,6 + η )
où,
- φ est l’humidité relative
- η la température
- pvs est la pression de saturation
| Exemple.
soit η= 16°C et φ = 53 % HR, on déduit : pv = (φ /100) . pvs = 0,53 . 102,7877 + (7,625 . 16) / (241,6 + 16) = 967,3 Pa h = 1,006 . 16 + 0,622 . (967,3 / (101 300 – 967,3)) . (2 501 + 1,83 . 16) = 31,3 kJ/kg |
Entre le volume spécifique, la température et l’humidité absolue
v = (461,24 . (0,622 + x) . T) / P
où,
- x est l’humidité absolue en kg eau / kg air sec
- T est la température absolue = η + 273,15°C
- P = pression totale de l’air humide, que l’on peut en première approche prendre égale à la pression atmosphérique, soit 101 300 Pa
| Exemple.
soit η = 25°C et x = 0,008 kgeau/kgair, v = (461,24 . (0,622 + 0,008) . (273,15 + 25)) / 101 300 = 0,855 m³/kg air sec |
Entre la température de rosée et la pression partielle de vapeur
Si η r > 0°C, ηr = 31,685 . x / (1 – 0,1311 . x)
Si ηr < 0°C, ηr = 27,952 . x / (1 – 0,1025 . x)
où,
- x = log 10 (pv / 613,34)
| Exemple.
soit η = 25°C et pv = 1 600 PA, alors : x = log 10 (1 600 / 613,34) = 0,416 ηr = 31,685 . 0,416 / (1 – 0,1311 . 0,416) = 13,9°C |
Entre la température bulbe humide et la pression partielle de vapeur
La relation suivante est empirique :
pv = pvsη h – K . P (η – η h)
où,
- pv est la pression partielle de vaporisation
- pvsηh est la pression de vapeur saturante correspondant à ηh
- K est une constante valant 6,6 x 10-4 pour η h > 0°C et 5,6 x 10 -4 pour ηh < 0°C
- P est la pression totale de l’air humide, que l’on peut en première approche prendre égale à la pression atmosphérique, soit 101 300 Pa
| Exemple.
soit la lecture suivante sur un psychromètre : η = 20°C et ηh = 15°C. Quelle est l’humidité relative dans la pièce ? pvs = 102,7877 + (7,625 . η ) / (241,6 + η) Si ηh = 15°C, pvs η h = 102,7877 + (7,625 . 15) / (241,6 + 15) = 1 711 PA </i.si> pv = pvs ηh – K . P (η- ηh) = 1 711 – 6,6 . 10-4 . 101 300 . (20 – 15) = 1 377 PA A 20°C, pvs = 102,7877 + (7,625 . 20) / (241,6 + 20) = 2 347 PA L’humidité relative est donc de : φ = pv / pvs = 1 377 / 2 347 = 59 % |
| T (°C) | pvs (Pa) |
ρvs (kg/m³) x10-3 |
xs (g/kg) |
| – 10 | 260 | 2,14 | 1,6 |
| – 9 | 284 | 2,33 | 1,75 |
| – 8 | 310 | 2,53 | 1,91 |
| – 7 | 338 | 2,75 | 2,08 |
| – 6 | 368 | 2,98 | 2,27 |
| – 5 | 401 | 3,24 | 2,47 |
| – 4 | 437 | 3,52 | 2,69 |
| – 3 | 476 | 3,81 | 2,94 |
| – 2 | 517 | 4,13 | 3,19 |
| – 1 | 562 | 4,47 | 3,47 |
| 0 | 611 | 4,84 | 3,78 |
| 1 | 657 | 5,19 | 4,07 |
| 2 | 705 | 5,56 | 4,37 |
| 3 | 759 | 5,95 | 4,70 |
| 4 | 813 | 6,35 | 5,03 |
| 5 | 872 | 6,79 | 5,40 |
| 6 | 935 | 7,25 | 5,79 |
| 7 | 1 002 | 7,74 | 6,21 |
| 8 | 1 073 | 8,26 | 6,65 |
| 9 | 1 148 | 8,80 | 7,13 |
| 10 | 1 228 | 9,38 | 7,63 |
| 11 | 1 313 | 10,00 | 8,15 |
| 12 | 1 403 | 10,70 | 8,75 |
| 13 | 1 498 | 11,40 | 9,35 |
| 14 | 1 599 | 12,10 | 9,97 |
| 15 | 1 706 | 12,80 | 10,6 |
| 16 | 1 818 | 13,60 | 11,4 |
| 17 | 1 938 | 14,50 | 12,1 |
| 18 | 2 065 | 15,40 | 12,9 |
| 19 | 2 197 | 16,30 | 13,8 |
| 20 | 2 340 | 17,30 | 14,7 |
| 21 | 2 487 | 18,30 | 15,6 |
| 22 | 2 645 | 19,40 | 16,6 |
| 23 | 2 810 | 20,60 | 17,7 |
| 24 | 2 985 | 21,70 | 18,8 |
| 25 | 3 169 | 23,00 | 20,0 |
| 26 | 3 362 | 24,40 | 21,4 |
| 27 | 3 565 | 25,80 | 22,6 |
| 28 | 3 781 | 27,20 | 24,0 |
| 29 | 4 006 | 28,70 | 25,6 |
| 30 | 4 244 | 31,70 | 27,2 |
Avec , ρv : la concentration de vapeur = le nombre de kg de vapeur d’eau par m³ d’air sec (kg/m³); ρvs , cette même valeur à la saturation.
Les valeurs pvs et xs ci-dessus peuvent également être trouvées par calcul à partir de la température.


![Degrés-jours [Théories – climat]](https://energieplus-lesite.be/wp-content/uploads/2019/03/energie-banner02_theories_02-500x383.png)



Auteur : les anciens
Mars 2009 : Thibaud
Notes :
[…] les isolants biosourcés qui nous intéressent ici possèdent des propriétés hygrothermiques prometteuses. Par leur capacité plus ou moins grande à absorber […]
[…] mais ça ne change pas grand chose à la forme de la courbe. Cette page sur les grandeurs hygrométriques m’a également bien […]
[…] distingue différentes classes de climat intérieur en fonction de la valeur annuelle moyenne de pression de vapeur d’eau pi à l’intérieur du […]