Sommaire


Le son et le spectre sonore
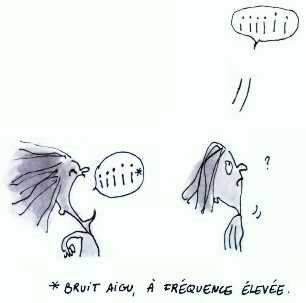
Qu’est-ce qu’un son ?
Le son est la sensation auditive engendrée par la fluctuation périodique de la pression de l’air.
Cette fluctuation se fait par rapport à la pression d’équilibre (la pression atmosphérique) et est ressentie au niveau de l’oreille.
Ainsi, une lame d’acier qui vibre entraîne la formation d’une succession de zones de pression et de dépression qui se propagent.
Cette variation de pression est sinusoïdale
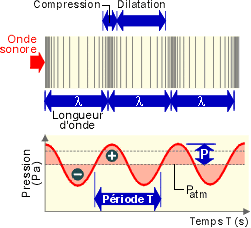
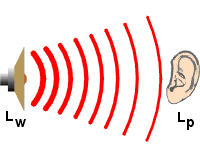
La variation de la pression se représente sous forme d’une onde sinusoïdale dont l’amplitude “P” caractérise le niveau de pression acoustique.
Cette amplitude traduit l’intensité de la sensation,et est encore appelée le niveau sonore. Elle est mesurée en Pascal [Pa]. C’est la pression exercée par l’onde sonore sur le récepteur (tympan, membrane d’un microphone, …).
Plus l’amplitude P est grande, plus le son est fort.
Et cette sinusoïde a une fréquence
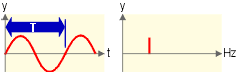
Un son pur (à une seule fréquence), qui présente une allure sinusoïdale en fonction du temps, se représentera seulement par un trait (dont la hauteur correspond à son amplitude P) dans un diagramme en fonction de la fréquence.
Le nombre de fluctuations par seconde définit la fréquence du son. Si la durée d’une fluctuation ou “période” est de T secondes, la fréquence sera de 1/T Hertz [Hz ou 1/s].
Ainsi, le “la” du diapason vibre à la fréquence de 440 Hz, sa période est donc de 2,3 millièmes de seconde.
Plus la fréquence 1/T est élevée, plus le son paraît aigu.
En réalité, nous vivons dans du bruit, mélange de multiples sons
Le son décrit au paragraphe ci-dessus est un son “pur”. En réalité, le bruit que nous entendons est généralement composé d’un mélange complexe de sons de fréquences et d’amplitudes différentes.
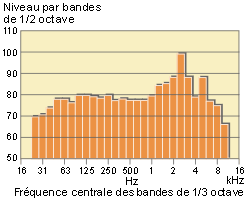
Spectre sonore d’un bruit, représentant l’amplitude des sons en fonction de leur fréquence.
(un octave est une bande de fréquence d’une largeur telle que la plus grande fréquence a une valeur double de la plus faible. 8 bandes d’octave sont définies en acoustique avec comme fréquence centrale : 62,5 Hz, 125 Hz, 250 Hz (sons graves), 500 Hz, 1 kHz(sons moyens), 2 kHz, 4 kHz, 8 kHz (sons aigus)).
Pour le représenter, il faut réaliser une analyse spectrale décrivant pour toutes les fréquences le niveau de pression acoustique : c’est le spectre sonore du bruit.
On précisera alors la hauteur du bruit : un bruit est plus ou moins haut (= aigu) suivant que sa fréquence dominante est plus ou moins élevée.
On distingue deux types de bruit dans le bâtiment : bruit aérien et bruit solidien (ou bruit d’impact)
 |
 |
Une source de bruit aérien (parole, radio, TV, …) produit dans l’air du local où elle se trouve, une onde se propageant en ligne droite jusqu’à ce qu’elle heurte une paroi.
Celle-ci est mise elle-même en vibration et transmet un son dans le local voisin.
 |
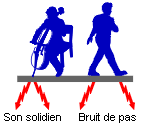 |
Par contre, un bruit d’impact est dû au choc d’un objet sur une paroi (meubles, pas, marteau sur un clou, …).
Au moment du choc, une quantité d’énergie importante est communiquée à la paroi (beaucoup plus que dans le cas d’un bruit aérien) et le son se propage facilement dans tout l’immeuble.
Le niveau sonore en décibels Lp
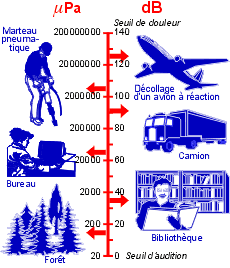
L’oreille est un organe extrêmement sensible ! Il perçoit des pressions acoustiques variant de 2.10-5 PA à 20 PA L’échelle varie donc de 1 à 1 000 000 !
Pour simplifier la mesure du niveau de pression acoustique, encore appelé “niveau sonore”, les acousticiens ont adopté une échelle logarithmique :
Lp = 10 log [p²/po²]
= 20 log [p/po]
où,
- p = pression acoustique mesurée
- po = pression acoustique de référence = 2.10-5 PA
- Lp est exprimé en décibels (dB)
Le décibel n’est donc pas une unité de mesure absolue mais est basée sur le rapport entre la pression mesurée et la pression de référence po. De plus, son évolution n’est pas linéaire, ce qui complique l’addition de 2 sons différents…
Mais ce mode de mesure correspond assez bien à la manière dont notre oreille entend et compare les sons !
Exemple.
20 x log [2 / 2 x 10 – 5] = 100 dB
20 x log [0,02 / 2 x 10 – 5] = 60 dB…
|
|
Rappel mathématique sur les propriétés des logarithmes log X = log10 X = y si X : 10y “Le logarithme en base 10 d’un nombre est l’exposant auquel il faut soumettre 10 pour retrouver le nombre”. ex : log (10) = 1 , log (100) = 2, … , log (10 000) = 4, … propriétés log (X.Y) = log X + log Y |
L’addition de niveaux sonores
Le problème de l’addition de plusieurs niveaux sonores se pose lorsque plusieurs sources sonores produisent un son simultanément. Comme les niveaux sonores sont des grandeurs logarithmiques, elles ne peuvent être additionnées comme telles.
Il faut soit repasser aux pressions correspondantes, soit utiliser le graphe ci-dessous qui donne l’accroissement D L en décibels à ajouter au niveau le plus élevé pour obtenir le niveau résultant, connaissant la différence L1 – L2 entre les 2 niveaux à composer.
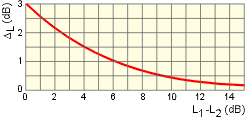
| Exemple.
Soit deux niveaux sonores L1 = 47 dB et L2 = 41 dB. Quel sera le son total perçu ? La différence L1-L2 = 47 – 41 = 6 dB. L’addition de ces deux sons donnera L1 + 2 = 47 + ΔL = 47 + 1 = 48 dB Curieux, non ? Cela provient de notre regard linéaire sur les valeurs 47 et 41 qui nous semblent proches. En réalité, l’expression du son en décibels utilise une échelle logarithmique : un son de 47 dB est en fait beaucoup plus élevé qu’un son de 41 dB. Et l’addition d’un son très faible à un son fort est considéré par notre oreille comme négligeable. (si la chaîne HiFi de notre ado génère 47 dB, il ne sera que peu perturbé par notre symphonie de Bach à 41 dB… C’est chouette pour lui non ?…). |
Application
On demande de déterminer le niveau global des 4 sources sonores suivantes : 84, 69, 82 et 78 dB.
Solution 1 : par calcul
L1 = 84 dB = 10 log [p1²/po²] › p1² = po².1084/10
L2 = 69 dB = 10 log [p2²/po²] › p2² = po².1069/10
L3 = 82 dB = 10 log [p3²/po²] › p3² = po².1082/10
L4 = 78 dB = 10 log [p4²/po²] › p1² = po².1078/10
› Ltot = 10 log [(p1² + p2² + p3² + p4²)/po²]
= 10 log (1084/10+1069/10+1082/10+1078/10)
= 86,8
Il faut donc faire attention de ne pas additionner les niveaux sonores mais bien les carrés des pressions acoustiques (on dit que les pressions s’ajoutent “quadratiquement”).
Solution 2 : par abaque
| L1 = 84 dB L2 = 69 dB |
L1 – L2 = 15 dB › Δ L = 0 dB L1 + 2 = 84 + 0 dB |
| L1 + 2 = 84 dB L3 = 82 dB |
L1 + 2 – L3 = 2 dB › Δ L = 2 dB L1 + 2 + 3 = 84 + 2 dB = 86 dB |
| L1 + 2 + 3 = 86 dB L4 = 78 dB |
L1 + 2 + 3 – L4 = 8 dB › Δ L = 1 dB L1 + 2 + 3 + 4 = Ltot = 86 + 1 = 87 dB |
| Remarque.
Deux sons de niveaux sonores identiques entraînent un son total de 3 dB plus élevé, tout juste perceptible. (par exemple, deux baffles d’une chaîne Hifi de 60 dB fourniront un son total de 63 dB… et, à distance, notre oreille aura difficile à percevoir si 1 ou 2 baffles fonctionnent !). Par ailleurs, pour deux enceintes qui diffuse le même signal, la sommation est de +6dB au centre, elle n’est de +3dB que si elles sont alimentées par des signaux décorréler, ce qui n’est vrai que si elles ont une différence de distance très grande en rapport a la longueur d’onde. |
En effet, Ltot = 10 log [(p1² + p2²)/po²] = 10 log 2 [p1²/po²]
= L1 + 10 log 2
= L1 + 3
La puissance acoustique Lw
On entend par puissance acoustique P la puissance d’une source sonore transmise sous forme de bruit aérien au milieu environnant. Comme pour la pression sonore, on utilisera la notion plus pratique de niveau de puissance acoustique Lw :
Lw = 10 log[P/Po]
où,
- P = puissance acoustique en Watt (W)
- po = puissance acoustique de référence = 10-12 W
Lw est également exprimé en décibels (dB). (Attention aux confusions avec le niveau sonore Lp !)
Le niveau de puissance acoustique est une valeur caractéristique de sources sonores (machines, haut-parleurs, …), alors que le niveau sonore en un lieu dépendra de l’éloignement de la source sonore, des caractéristiques de réverbération de la pièce, …
|
Source sonore |
P (W) | Lw (dB) |
Source sonore |
P (W) | Lw (dB) | |
| Bruissement des feuilles | 1.10-9 | 30 | radio bruyante | 1.10-1 | 110 | |
| Chuchotement | 1.10-8 | 40 | klaxon, marteau pneumatique | 1 | 120 | |
| Conversation à voix basse | 1.10-7 | 50 | grand orchestre | 10 | 130 | |
| Conversation normale | 1.10-5 | 70 | hélice d’avion | 1.103 | 150 | |
| Conversation à haute voix | 1.10-4 | 80 | réacteur d’avion | 1.105 | 170 | |
| – | fusée Saturne | 4.107 | 195 |
Différence entre puissance acoustique et niveau sonore
Il est important de comprendre la différence entre puissance acoustique et pression acoustique (= pression sonore), car les documents techniques abordent ces deux notions…
| Exemple. l’écouteur d’un baladeur est de très faible puissance acoustique, mais peut engendrer une pression sonore très élevée lorsqu’il est situé à quelques millimètres du tympan ! |
Une analogie existe entre lumière et son :
| Quel éclairage donnera cette ampoule ? | Quel bruit fera ce climatiseur ? | |
| L’éclairage dépend de la puissance lumineuse de la lampe. | Le bruit dépend de la puissance sonore de la source Lw. | |
| Le niveau d’éclairement en un endroit de la pièce est donné en lux. | Le niveau de pression acoustique Lp en un endroit de la pièce est donné en décibel. | |
|
|
|
|
| Plus on s’éloigne de la lampe, plus le niveau d’éclairement diminue. | Plus on s’éloigne de la source, plus le niveau de pression sonore diminue. | |
| Pour une lampe donnée, le niveau d’éclairement est plus élevé dans une petite pièce que dans un grand local. | Pour une source sonore donnée, le niveau de pression sonore est plus élevé dans une petite pièce que dans un grand local. | |
| Le niveau d’éclairement est plus élevé dans une pièce avec des murs blancs réfléchissants qu’avec des murs sombres. | Le niveau de pression acoustique est plus élevé dans une pièce à parois lisses (béton, par ex.) qu’avec des parois absorbantes (tapis, p.ex.). |
Lien entre puissance acoustique et niveau sonore
Le niveau de puissance acoustique est une valeur caractéristique des sources sonores (machines, haut-parleurs, …). Pour une puissance acoustique donnée, la pression acoustique dans le local va dépendre du milieu qui entoure la source et de la position du point de mesure. Plus on s’éloigne de la source sonore, plus la pression acoustique décroît. Elle va dépendre également des qualités d’absorption des parois.
On pourrait établir une analogie avec une lampe d’éclairage : elle possède une puissance donnée mais le niveau d’éclairement dépend de la distance à laquelle on se trouve de la lampe. De plus, le niveau d’éclairement (= de pression acoustique) est plus élevé dans une pièce dont les murs sont blancs (= dont les murs sont réfléchissants) que lorsque les murs sont sombres (= dont les murs sont absorbants).
En première approximation , le lien entre Lp et Lw peut s’établir par différentes relations empiriques :
Relation 1 :
Lp = Lw – 5 log V – 10 log r + 3 [dB]
où,
- V est le volume de la pièce et r la distance entre émetteur et récepteur.
Cette relation ne s’applique qu’aux locaux “normaux”, c’est-à-dire ni trop réverbérants ou ni trop sourds.
| Exemple.
Dans un bureau de 75 m3 , quel est le niveau de pression sonore engendré par un climatiseur dont la puissance sonore est de 50 dB, aux oreilles de la secrétaire située à 3 m de l’appareil ? Réponse. 39 dB car Lp = 50 – 5.log(75) – 10.log(3) + 3 |
Relation 2 :
Lp = Lw – 10 log V + 10 log T + 14 [dB]
où,
- V est le volume de la pièce et T le temps de réverbération du local.
| Exemple.
Dans un bureau de 75 m3 et dont le temps de réverbération est de 0,8 sec, quel est le niveau de pression sonore engendré par un climatiseur dont la puissance sonore est de 50 dB, aux oreilles de la secrétaire ? Réponse. 44 dB car Lp = 50 – 10.log(75) + 10.log(0,8) + 14 |
La comparaison des deux résultats montre qu’il n’est pas simple de donner cette relation (comme il n’est pas simple de donner l’éclairement d’un point du local si les couleurs des parois ne sont pas connues…).
D’une manière approchée, on a souvent :
Lp = Lw – 5…10 [dB]
Relation 3 :
A l’extérieur, la relation entre puissance acoustique et pression acoustique est donnée par :
Lp=Lw+10*log(Q/(4.π.r2)) [dB]
où,
- r est la distance à la source
- Q est le facteur de directivité : il s’agit de l’inverse de la fraction d’espace dans lequel la source transmet son énergie :
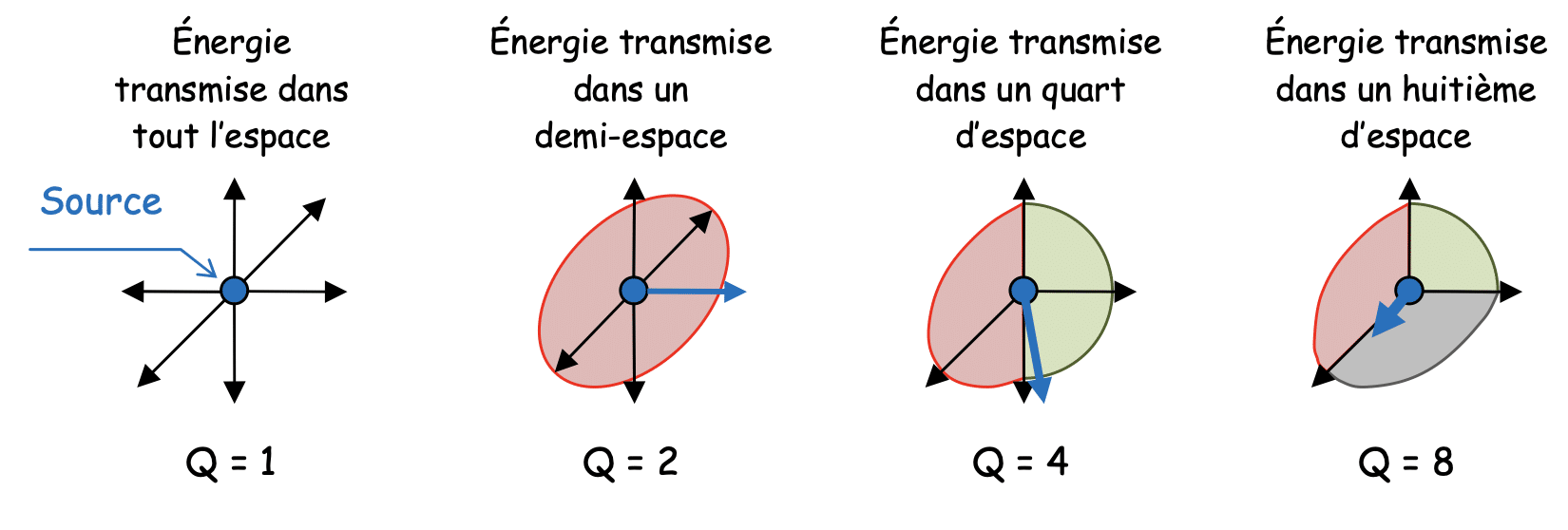
Illustration du facteur de directivité pour le calcul de la pression acoustique
Coefficient d’absorption
Tous les matériaux absorbent plus ou moins d’énergie sonore. Le coefficient d’absorption précise le rapport entre l’énergie acoustique absorbée et l’énergie incidente.
| Exemple.
Si local de bureau possède un coefficient d’absorption moyen de 0,2, chaque fois qu’un son frappe une paroi, il est absorbé de 20 %. |
Une paroi lisse, dure et lourde est très réfléchissante : son coefficient d’absorption a est proche de 0. Par contre, les matériaux fibreux, à porosité ouverte, auront un coefficient d’absorption a proche de 1, du moins pour les hautes fréquences. Car il faut distinguer la capacité d’absorption des matériaux en fonction de la fréquence.
Le fabriquant d’un matériau absorbant fournira un diagramme du type repris ci-dessous (c’est le spectre d’absorption) :
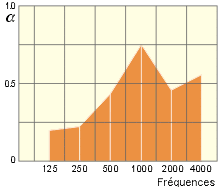
Le tableau ci-dessous fournit des coefficients d’absorption typiques de matériaux.
|
Élément |
Facteur d’absorption α (moyennes de bande d’octave) |
|||||
| 125 Hz | 250 Hz | 500 Hz | 1 000 Hz | 2 000 Hz | 4 000 Hz | |
| Crépis lisse sur maçonnerie ou béton | 0,01 | 0,01 | 0,02 | 0,02 | 0,03 | 0,04 |
| Plafond de plâtre suspendu, lisse | 0,25 | 0,2 | 0,1 | 0,05 | 0,05 | 0,1 |
| Revêtement de paroi en bois ou panneau de bois aggloméré sur lattage | 0,4 | 0,3 | 0,2 | 0,1 | 0,1 | 0,2 |
| Revêtement de sol collé (bois, liège, caoutchouc) | 0,02 | 0,03 | 0,04 | 0,05 | 0,05 | 0,1 |
| Parquet etc. sur faux plancher | 0,2 | 0,15 | 0,1 | 0,1 | 0,05 | 0,1 |
| Moquettes d’épaisseur moyenne | 0,05 | 0,08 | 0,2 | 0,3 | 0,35 | 0,4 |
| Rideaux (qualité moyenne) | 0,1 | 0,15 | 0,3 | 0,4 | 0,5 | 0,6 |
| Panneau acoustique de 2 cm, collé | 0,1 | 0,15 | 0,4 | 0,6 | 0,7 | 0,7 |
| Panneau acoustique de 2 cm, sur lattage | 0,2 | 0,3 | 0,6 | 0,7 | 0,7 | 0,7 |
| Fenêtre fermée | 0,1 | 0,04 | 0,03 | 0,02 | 0,02 | 0,02 |
| Surface occupée par des spectateurs, un orchestre ou des chœurs | 0,60 | 0,74 | 0,88 | 0,96 | 0,93 | 0,85 |
| Surface des sièges (rembourrage de tissu tendu, sans spectateurs | 0,49 | 0,66 | 0,80 | 0,88 | 0,82 | 0,70 |
| Surface des sièges (rembourrage de cuir) sans spectateurs | 0,44 | 0,54 | 0,60 | 0,62 | 0,58 | 0,50 |
En général, on considère un coefficient d’absorption moyen par local de :
- 0,4 pour des locaux très absorbants (salles de concerts, cinémas,…)
- 0,2 pour des locaux moyennement absorbants (bureaux, habitations, …)
- 0,1 pour des locaux réverbérants (églises, ateliers, salles de sports,…)
Le temps de réverbération
Lorsque cesse l’émission d’un bruit dans une salle fermée, il subsiste pendant un moment une traînée sonore. Cette traînée est longue si le volume du local est grand, si les parois sont lisses, nues et parallèles deux à deux. On dit qu’il y a une importante “durée de réverbération”.
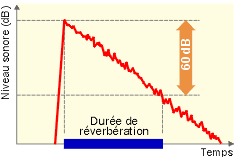
Pour la mesure, on a fixé la durée de réverbération T au temps correspondant à une décroissance de 60 dB du niveau sonore après l’arrêt du fonctionnement de la source.
Supposons que l’on tapisse les parois d’un épais matelas fibreux. Dès que la source cesse d’émettre, on n’entend plus rien : on dit que la salle est sourde. Le temps de réverbération est court.
Le temps de réverbération évolue dans la plupart des locaux entre 0,5 et 1 seconde.
Comment évolue le temps de réverbération en fonction des parois d’un local ?
La formule empirique de Sabine détermine le temps de réverbération T (en secondes) :
T = (0,16 xa V) / A [s]
où,
- V = volume du local (m³),
- A = surface d’absorption équivalente de la salle (m²)
avec A = Somme des Si * αi de toutes les parois du local,
- où Si = surface couverte par le matériau i (m²),
- αi = coefficient d’absorption moyen du matériau i.
Par exemple, un mètre carré de matériau de facteur d’absorption a = 0,5 sera équivalent à 0,5 m² de surface parfaitement absorbante.


Auteur : les anciens
Notes :