Sommaire

Coefficient de résistance à la diffusion de vapeur d’un matériau
Le mouvement de diffusion de vapeur sera d’autant plus important que le matériau constituant la paroi sera plus perméable à la vapeur c’est à dire que son coefficient de résistance à la diffusion de vapeur est faible.
Le coefficient de résistance à la diffusion de vapeur μ d’un matériau μ indique dans quelle mesure, la vapeur d’eau traverse plus difficilement ce matériau que l’air. La valeur μ d’un matériau est toujours supérieure à 1.
La quantité de vapeur d’eau diffusant à travers une couche d’un matériau déterminé ne dépend pas uniquement de la valeur µ du matériau mais aussi de l’épaisseur de cette couche. L’épaisseur équivalente de diffusion μd (ou Sd) indique la résistance qu’offre une couche de matériau à la diffusion de vapeur d’eau. µd est le produit du coefficient de résistance à la diffusion de vapeur (μ ) par l’épaisseur du matériau (d) et s’exprime en mètres.
Le µd d’une couche de matériau correspond à l’épaisseur en m de la couche d’air stationnaire qui exercerait la même résistance à la diffusion de vapeur que la couche de matériau.
| Exemple.
Lorsque le µ d’un matériau vaut 5, cela signifie :
Le coefficient de résistance à la diffusion de vapeur de certains matériaux dépend de leur état : sec ou humide. |
Valeurs indicatives
| Quelques valeurs de µ[1]Ministère de la Région Wallonne, Isolation thermique des logements neufs en région wallonne. Caractéristiques hygrothermiques des matériaux. Édition 88.002. |
|||
| Matériau | Densité kg/m³ | µ sec | µ humide |
|
Air |
1 |
||
| Métaux | infini | ||
|
Granit, basalte, porphyre, marbre |
infini | infini | |
|
Pierre bleue (petit granit) |
infini | infini | |
|
Schiste ardoisier |
> 600 | ||
|
Pierre ferme |
2 160 – 2 349 | 70 – 90 | |
|
Pierre tendre |
1 650 – 1 839 | 26 – 32 | |
| 1 100 – 1 500 | 5 – 10 | 5 – 10 | |
|
Maçonnerie de briques, légère |
700 – 1 000 | 5 – 10 | |
|
Maçonnerie de briques, moyenne |
1 300 | 7.5 | |
| 1 500 | 8 | ||
|
Maçonnerie de briques, lourde |
1 700 – 1 900 | 9 – 14 | |
| 2 100 | 31 | ||
|
Blocs pleins de béton cellulaire |
500 – 549 | 6 | 3 |
|
Blocs pleins de béton cellulaire |
600 – 699 | 10 | 6 |
|
Blocs pleins de béton très léger |
500 – 800 | 5 – 10 | |
|
Blocs pleins de béton mi-lourd |
< 1 400 | 5 – 10 | |
| > 1 401 | 10 – 15 | ||
|
Maçonnerie en briques silico-calcaire |
< 1 400 | 5 – 10 | |
| > 1 400 | 15 – 25 | ||
| 2 000 | 25 | ||
|
Maçonnerie en blocs de plâtre |
9 | 6 | |
|
Béton plein très léger |
200 | 2.8 | |
| 300 | 3.5 | ||
| 500 | 4.5 | ||
|
Béton plein léger |
700 | 5.5 | |
|
Béton plein moyennement léger |
1 000 | 6.5 | |
| 1 30 | 7.5 | ||
| 1 600 | 8 | ||
|
Béton plein lourd |
1 900 | 13 | |
| 2 300 | 135 | 30 | |
|
Béton lourd non compacté non armé |
2 200 | 23 – 200 | |
| 2 400 | 31 – 200 | ||
|
Béton lourd non compacté, armé |
2 300 | 27 – 200 | |
|
Béton lourd compacté, armé |
2 500 | 37 – 200 | |
|
Béton plein isolant |
300 – 700 | 4.5 – 5.5 | |
|
Béton plein de granulats EPS |
350 – 400 | 7.5 – 11 | |
|
Béton plein cellulaire |
400 – 750 | 3.7 – 6.5 | |
|
Béton plein cellulaire |
400 | 3 – 7.5 | |
| 480 | 6 | 3 | |
| 600 | 11 | 5 | |
| 700 | 4.5 – 7.5 | ||
| 1 000 | 5.5 – 7.5 | ||
| 1 300 | 7.5 – 9 | ||
|
Béton plein d’argile expansé |
550 – 1 000 | 5 – 6.5 | |
| 1 000 – 1 800 | 6.5 – 12 | ||
|
Béton plein de bims |
700 – 1 000 | 6 | |
| 1 000 – 1 400 | 6.5 – 12 | ||
|
Béton plein à base de granulés d’argile expansé |
900 – 1 000 | 10 – 16 | 10 – 16 |
|
Béton plein de laitier de haut fourneau |
1 000 | 6.5 | |
| 1 300 | 8 | ||
| 1 600 | 10 | ||
| 1 900 | 14 | ||
|
Béton plein de laitier de haut fourneau + sable du Rhin |
1 500 | 10 | |
| 1 700 | 40 | ||
| 1 900 | 60 | ||
|
Béton plein aggloméré “en granulés” |
2 100 | 18 | 16 |
|
Enduit en mortier de ciment |
15 – 41 | ||
|
Enduit en mortier de chaux |
9 – 41 | ||
|
Enduit en plâtre |
6 – 10 | ||
|
Enduit de résine synthétique |
10 – 125 | ||
|
Saule, bouleau, hêtre tendre |
120 | 18 | |
|
Teck |
37 – 370 | ||
|
Chêne, hêtre, frène, noyer, méranti |
370 | 40 | |
|
Pin |
370 | 9 | |
|
Epicéa |
9 – 370 | ||
|
Sapin rouge du Nord, Orégon |
120 | 18 | |
|
Bois résineux |
18 – 120 | ||
|
Sapin |
18 – 120 | ||
|
Pitchpine |
370 | 40 | |
|
Multiplex |
400 – 499 | 16 | |
| 500 – 599 | 175 | 50 | |
| 700 | 40 – 100 | ||
| 800 | 50 – 400 | ||
|
Contreplaqué marin |
1 000 | 46 – 75 | |
|
Panneau de particules type tendre |
< 300 | 5 | |
|
Panneau de copeaux colle U.F. |
550 – 700 | 40 – 140 | +/- 25 |
|
Panneau de copeaux colle mélam. |
550 – 700 | 30 – 100 | +/- 30 |
|
Panneau de copeaux colle P.F. |
600 – 700 | 50 – 150 | +/- 20 |
|
Panneau de particules type lourd |
1 000 | 46 – 75 | |
|
Panneaux de fibre de bois au ciment |
3.7 – 10 | 4 | |
|
Laine minérale |
1.1 – 1.8 | ||
|
Liège expansé |
4.5 – 29 | ||
|
Liège expansé imprégné |
9 – 46 | ||
|
Polystyrène expansé |
15 – 150 | ||
|
Polystyrène extrudé avec peau de surface |
115 – 300 | ||
|
Mousse de polyuréthane |
23 – 185 | ||
|
Perlite expansée pure |
50 – 80 | 1.5 | |
|
Perlite expansée en panneau |
170 | 7 | 5 |
|
Vermiculite expansée pure |
80 – 100 | 1.5 | |
|
Vermiculite expansée en panneau |
350 | 8 | |
|
Verre cellulaire en plaque |
70 000 – infini | ||
|
Verre cellulaire en granulés |
1.5 | ||
|
Verre |
infini | ||
|
Céramique de verre |
infini | ||
|
Carreaux de céramique |
150 – 300 | ||
|
Caoutchouc |
900 | ||
|
Linoléum |
1 800 | ||
|
Asbeste-ciment |
800 | 14 | |
| 1 600 – 1 900 | 37 – 150 | ||
|
Bitume oxydé |
70 000 – 120 000 | ||
|
Feutre bitumé |
15 000 | ||
|
Polyisobuthylène |
80 000 – 260 000 | ||
|
EPDM |
65 000 | ||
|
Butyl |
300 000 | ||
|
PVC |
20 000 – 40 000 | ||
|
Feutre bitumé, goudronné et sablé |
50 | ||
|
Voile de verre bitumé |
20 – 180 | ||
|
Tuiles de terre cuite |
36 – 44 | ||
|
Vernis d’adhérence |
400 – 900 | ||
|
Papier |
100 | ||
|
Feuille de PVC |
10 000 – 100 000 | ||
|
Feuille de polyisobutylène |
360 000 | ||
|
Feuille de Polyester |
13 000 | ||
|
Feuille de Polyéthylène |
50 000 – 320 000 | 285 000 | |
Résistance à la diffusion de vapeur d’une paroi homogène et calcul de la densité de flux de vapeur à travers cette paroi (régime stationnaire)
Considérons la diffusion de vapeur à travers une couche de matériau plane et homogène d’une épaisseur d; diffusion résultant d’une différence de pression partielle de vapeur.
- A = superficie (m²),
- pv1 = pression de vapeur à la face intérieure (Pa),
- pv2 = pression de vapeur à la face extérieure (Pa)
pv1 > pv2 (Conditions hivernales)
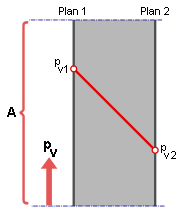
La différence de pression de vapeur (pv1 – pv2) entraîne une diffusion de vapeur d’eau de l’intérieur vers l’extérieur.
Question : quelle est la quantité de vapeur diffusant du plan 1 vers le plan 2 en t secondes, à travers une surface A (m²) ?
Par intuition, on sait que la quantité de vapeur Qd cherchée sera :
- directement proportionnelle à la surface considérée A (m²),
- directement proportionnelle à la différence de pression de vapeur (pv1 – pv2) (Pa),
- directement proportionnelle à la durée de temps considérée t (s),
- inversément proportionnelle à l’épaisseur du matériau d (m),
- inversément proportionnelle au coefficient de résistance à la diffusion μ .
Si l’on exprime ces considérations par une formule, on obtient :
Qd = directement proportionnelle à![]()
Pour compléter la formule, l’expression “directement proportionnelle à”, est remplacée par un coefficient de proportionnalité représenté par la lettre C.
La formule devient alors :
![]() (1)
(1)
On peut appliquer la formule (1) non pas à A (m²) mais à 1 m² et non pas à une durée t(s) mais pour 1 s :
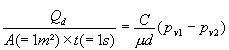
La grandeur Qd/A x t est appelée densité du flux de vapeur d’eau (kg/(m² x s)).
La densité du flux de vapeur d’eau est représentée par le symbole qd. Nous avons donc :
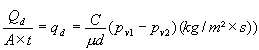 (2)
(2)
La densité du flux de vapeur qd indique donc la quantité de vapeur d’eau qui traverse la paroi par m² de surface et par seconde.
Les dimensions de C sont :
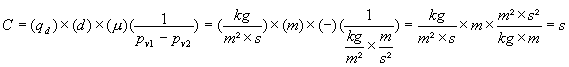
Ainsi, C s’exprime en secondes (s).
Dans les conditions telles qu’on les rencontre normalement dans les bâtiments, on peut considérer C comme étant une constante :
C = 0,185 x 10 – 9 s (ou : N = 1/C = 5,4 x 109 s – 1)
La formule (2) s’écrit :
![]() ou
ou ![]() (3)
(3)
(5,4 x 109 x μd) est appelé la résistance à la diffusion Z.
Cette valeur très élevée de la constante de diffusion signifie que la résistance à la diffusion de tout matériau est, en fait, très élevée et que les quantités de vapeur transportées par diffusion seront très faibles.
La relation (3) s’écrit alors :
![]()
Une résistance à la diffusion Z très élevée conduit à un faible flux de vapeur.
Remarque.
On peut obtenir une résistance à la diffusion très élevée en utilisant soit une couche mince d’un matériau ayant une valeur μ très élevée (= PARE-VAPEUR), soit une couche épaisse d’un matériau ayant une valeur μ peu élevée.
| Exemple : la paroi homogène.
Une Paroi en briques silico-calcaires (ρ= 1 800 kg/m³) a une valeur La densité du flux de vapeur d’eau vaut :
|
Résistance à la diffusion de vapeur d’une paroi composite
Généralement, une paroi se compose de plus d’une couche. La résistance à la diffusion totale d’une paroi composite s’obtient en faisant la somme des résistances à la diffusion des couches constituantes.
Zt = Z1 + Z2 + Z3 + Zn = ΣZk
ou Zt = 5,4 x 109 x (μ1d1 + μ 2d2 + … μn x dn)
Tout comme dans le cas du transfert de chaleur, la vapeur d’eau doit vaincre une certaine résistance en passant d’une paroi vers l’air ambiant et inversement. Toutefois, ces résistances de passage sont si faibles que l’on n’en tiendra pas compte.
Finalement, la formule devient :
![]() kg/(m² x s)
kg/(m² x s)
dans laquelle,
- pvi = pression de vapeur intérieure (Pa)
- pve = pression de vapeur extérieure (Pa)
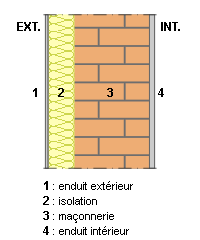
| Exemple : la paroi composite.
Considérons le transport de chaleur à travers une paroi composite constituée de l’intérieur vers l’extérieur comme suit :
Supposons qu’à l’intérieur, l’humidité relative est de 50 % à 22°C et à l’extérieur, de 70 % à – 5°C. Calculons la quantité de vapeur d’eau qui diffuse dans la paroi et l’évolution de la pression de vapeur. Données de base :
La résistance à la diffusion totale est de : 5,4 x 109 x Sμd= 5,4 x 109 x 2,23 = 12 x 109 m/s Les valeurs des pressions de vapeur maximales à 22°C et – 5°C sont respectivement de 2 645 et 401 Pa. Les pressions sont donc : pvi = 2 645 x 50 % = 1 322 Pa Ce qui donne :
|
Évolution de la pression de vapeur dans une paroi composite (régime stationnaire)
Comme pour le transfert de chaleur, l’évolution de la pression de vapeur dans chaque couche de la paroi est rectiligne si l’on se trouve en régime stationnaire. Pour une paroi composite, il suffit donc de calculer les pressions de vapeur au droit des interfaces des différentes couches et de relier les points ainsi obtenus par des droites.
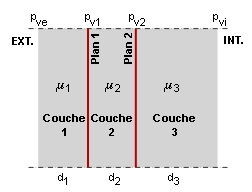
La formule suivante :
![]() permet de calculer qd
permet de calculer qd
La formule qd générale peut aussi être appliquée séparément à chacune des couches :
couche 1 :![]()
couche 2 : ![]()
couche 3 : ![]()
En régime stationnaire, les quantités qd1,qd2, qd3 et qd doivent être égales. En effet, si qd1 était supérieur à qd2, la quantité de vapeur d’eau quittant le plan 1 serait supérieure à celle qui y arrive et, dans ce cas, la pression de vapeur au droit du plan 1 (pv1) ne pourrait rester constante.
Tout plan parallèle est donc traversé par la même quantité d’humidité ou :
qd = qd1 = qd2 = qd3
donc :
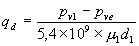 =
= ![]() =
= ![]() =
=![]()
Nous pouvons en déduire pv1 et pv2 :
![]()
![]()
D’une manière générale, on peut en fait écrire :
|
|
| Exemple : la toiture.
Considérons une toiture constituée de la manière suivante : une structure portante en béton, épaisseur = 120 mm, (μ = 80), un matériau isolant, épaisseur = 50 mm, (μ = 40), une couverture de toiture, μd = 100 m. Les températures sont de – 5 °C à l’extérieur et + 20 °C à l’intérieur. Les humidités relatives respectives sont de 70 % et 50 %. – 5 °C –> pvse = 401 PA, q = 70 % –> pve = 281 Pa Reprenons les données sous forme de tableau :
Z = 5,4 x 109 x 111,6 = 603 x 109 m/s. Si nous comparons les valeurs μd, nous voyons que 90 % environ du gradient de tension de vapeur apparaît au droit de la couverture. Les 10 % restants concernent l’isolation et la structure portante. L’évolution de la tension de vapeur est schématisée ci-après.
Pour qd, nous trouvons :
|
Remarque importante.
- Dans les deux exemples précédents, le résultat n’est exact que pour autant que la tension de vapeur calculée ne dépasse, en aucun endroit de la paroi, la tension maximale.
- Dans le cas contraire, il y aurait condensation.
Sources
 égale à 15 (-) et une épaisseur de 20 cm. La pression de vapeur extérieure est de 280 Pa et la pression de vapeur intérieure de 1 320 PA.
égale à 15 (-) et une épaisseur de 20 cm. La pression de vapeur extérieure est de 280 Pa et la pression de vapeur intérieure de 1 320 PA.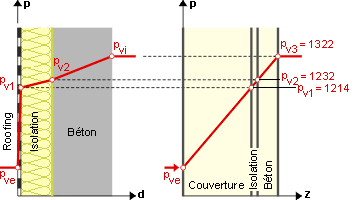



Auteur :
Notes :
Antidote :