Sommaire

Préambule
Données météorologiques récentes : Un climat en mutation
Révolution technologique : au-delà de l’anémomètre
Impact du Changement Climatique : Vers de Nouveaux Paradigmes
Conclusion
Mesurer le vent
Mesure de l’amplitude de la vitesse

Cette mesure est typiquement réalisée par un anémomètre à coupelle. Une coupelle présente une résistance au vent différente suivant la direction du vent : du coté du dos profilé, la résistance est moindre qu’avec la partie creuse face au vent. Les trainées sur les différentes coupelles de l’anémomètre auront une même direction (orientée avec la vitesse du vent) mais une amplitude différente. Cela va mettre le rotor de l’anémomètre en mouvement. Naturellement, la vitesse de rotation sera d’autant plus importante que la vitesse du vent est grande. Il y aura donc une relation directe entre la vitesse de rotation et la vitesse du vent. Un peu d’électronique embarquée permet de faire cette conversion et de stocker les données mesurées pendant la période d’observation (data logger).
Mesure de la direction du vent
La direction du vent peut se faire par une simple girouette. Celle-ci est souvent combinée à l’anémomètre comme il est illustré dans la figure ci-dessus.
Mesure au bon endroit et à la bonne hauteur
La vitesse du vent dépend fortement de l’emplacement, c’est pourquoi il est important de réaliser la mesure du vent le plus près possible du lieu de la future implantation des éoliennes. On peut se poser la question de savoir si au sein de la future parcelle de terrain, il est vital de placer le capteur à l’endroit exact des futures éoliennes. Cela doit dépendre fortement de la taille de l’éolienne et de la nature du terrain. Plus l’éolienne est petite et plus elle est sensible à des variations locales. De même, la nature du terrain a de l’importance. En effet, si on est en présence d’un terrain plat sans obstacles, la position de la mesure ne doit pas être très critique : l’évolution du champ de vitesse le long du terrain doit être régulière. Par contre, en présence d’irrégularités, comme des obstacles, le choix de la position de mesure doit être plus sensible. En conclusion, il est difficile de donner une règle précise, mais ces éléments de réponse devraient permettre de choisir le plus judicieusement possible ses points de mesure.
On a aussi mis en évidence la forte dépendance de la vitesse moyenne du vent avec la hauteur. Il est donc important de placer le capteur de mesure le plus prêt possible de la future hauteur du rotor de l’éolienne. On réalise cela au moyen d’un mât de mesure. Il faut être vigilant à la législation en vigueur, sur la possibilité d’ériger un tel mât sur votre terrain.
Que se passe-t-il si le mât n’est pas à la même hauteur ? Comme il a été expliqué dans la section relative sur la dépendance de la vitesse avec la hauteur, il y a moyen de déduire la vitesse à une autre hauteur, h, en fonction de la mesure de référence réalisée à la hauteur, h0. Cette relation n’est uniquement valable que si on est en présence d’un terrain plat, homogène et sans obstacle :
V(h) = V(h0) (h/h0)α
avec le coefficient “alpha” qui dépend de la rugosité du sol sur le terrain considéré. En fait, il s’agit de la rugosité du sol telle que vue par le vent, c’est-à-dire le type de couverture (eau calme, herbe, arbres, …). Les valeurs du coefficient “alpha” sont données ici à titre d’exemple.
Le vent en Belgique
Le vent est un déplacement d’air, essentiellement horizontal, d’une zone de haute pression (masse d’air froid) vers une zone de basse pression (masse d’air chaud). Les différences de température entre les masses d’air résultent de l’action du soleil. Le régime des vents en un lieu est représenté par une rose des vents, qui exprime la distribution statistique des vents suivant leur direction. Par définition, la direction d’un vent correspond à son origine.
C’ est un facteur climatique important dans la détermination des besoins en énergie d’un bâtiment. Il influence le taux d’infiltration d’air du bâtiment, ainsi que les échanges de chaleur par convection à la surface de l’enveloppe des bâtiments peu isolés.
Par exemple, si à un certain moment de la journée l’intensité du vent augmente et que sa direction passe à l’ouest, le ciel se couvrira de nuages et le taux d’infiltration d’air du bâtiment augmente. Ainsi, s’il fait froid, les déperditions thermiques et donc les besoins en énergie de chauffage des locaux augmentent.
Cela suppose de connaître d’une part, la fréquence et la vitesse moyenne du vent dans toutes les directions et d’autre part, pour toutes directions confondues, la fréquence des différentes plages d’intensité du vent.
| La direction et la vitesse du vent caractérisent celui-ci. La direction du vent en un lieu est donnée par l’orientation d’où il souffle; la vitesse du vent est exprimée en km/h. |
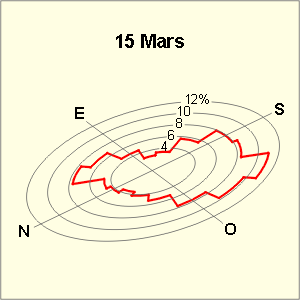
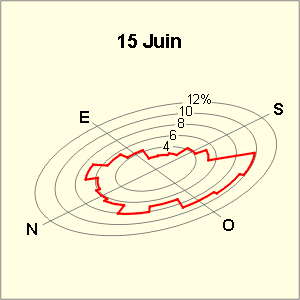
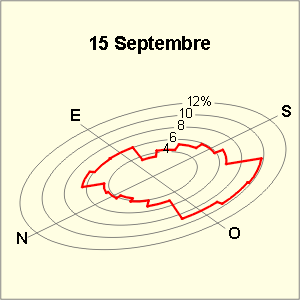
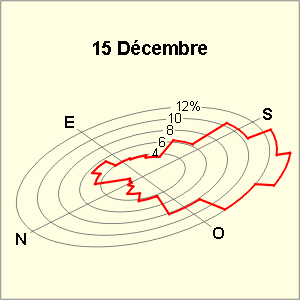
Les graphes et tableaux ci-dessous donnent, pour chaque direction du vent, la fréquence en % du temps et la vitesse moyenne, le 15 des mois de mars, juin, septembre et décembre, à Uccle.
|
Direction |
Fréquence |
Vitesse km/h |
| N N N E N E E N E E E S E S E S S E S S S O S O O S O O O N O N O N N O |
4,2 4,6 7,7 6,6 4,6 2,9 3,3 5,6 7,9 8,4 11,0 9,7 7,7 5,3 4,2 3,6 |
17,6 17,1 15,6 13,6 12,9 16,6 14,0 16,9 19,8 21,3 22,6 22,3 17,5 16,5 14,7 14,8 |
|
Direction |
Fréquence |
Vitesse |
| N N N E N E E N E E E S E S E S S E S S S O S O O S O O O N O N O N N O |
6,2 5,8 7,0 5,4 4,3 2,4 2,5 2,8 4,2 5,3 10,0 9,6 9,2 7,1 8,1 6,6 |
13,5 13,5 12,4 11,1 9,7 8,5 9,1 10,9 12,3 13,4 15,0 14,4 12,4 11,6 11,1 12,0 |
|
Direction |
Fréquence |
Vitesse |
| N N N E N E E N E E E S E S E S S E S S S O S O O S O O O N O N O N N O |
4,2 4,4 6,4 5,9 6,0 3,3 4,3 5,2 5,9 6,7 9,9 9,8 9,0 5,2 4,2 3,7 |
13,4 11,0 12,0 11,6 10,3 8,8 10,0 11,3 12,1 13,6 13,7 12,6 12,1 11,7 10,3 11,1 |
|
Direction |
Fréquence |
Vitesse |
| N N N E N E E N E E E S E S E S S E S S S O S O O S O O O N O N O N N O |
1,3 1,2 4,5 5,4 4,0 3,8 3,4 6,3 10,5 12,8 14,2 12,0 8,8 4,4 3,0 1,7 |
15,4 17,0 15,6 13,9 11,5 6,3 15,9 17,9 20,2 20,5 22,0 20,5 19,0 18,9 16,7 14,0 |
Par exemple, la fréquence et la vitesse moyenne du vent est de :
- 9,7 % et 22,3 km/h pour la direction OSO le 15 mars,
- 6,4 % et 12 km/h pour la direction NE le 15 septembre,
- 14,2 % et 22 km/h pour la direction SO le 15 décembre.
Afin de tenir compte de l’intensité du vent à considérer dans les calculs de déperditions thermiques des bâtiments, le tableau ci-dessous donne les fréquences du vent correspondant aux plages de vitesse de 10 en 10 km/h, toutes directions confondues, à Uccle.
| Vitesse |
Fréquence en % du temps |
|||||||||||
| km/h | J | F | M | A | M | J | J | A | S | O | N | D |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 – 9 | 27,7 | 30,7 | 30,5 | 31,3 | 40,8 | 45,0 | 49,9 | 46,4 | 50,3 | 43,8 | 36,8 | 29,7 |
| 10 – 19 | 33,3 | 34,1 | 36,0 | 38,1 | 41,1 | 41 | 37,9 | 38,4 | 37,6 | 35,2 | 34,7 | 32,5 |
| 20 – 29 | 24,0 | 20,9 | 20,1 | 21,8 | 14,9 | 11,5 | 10,2 | 12,2 | 10,2 | 11,5 | 18,6 | 22,8 |
| 30 – 39 | 10,0 | 9,5 | 0,9 | 6,7 | 2,8 | 2,1 | 1,7 | 2,5 | 1,4 | 4,1 | 6,7 | 10,2 |
| 40 – 49 | 3,6 | 3,4 | 3,3 | 1,8 | 0,4 | 0,4 | 0,2 | 0,4 | 0,3 | 1,2 | 2,6 | 3,6 |
| > 50 | 1,3 | 1,3 | 1,1 | 0,2 | 0 | 0 | 0 | 0 | 0 | 0,2 | 0,4 | 1,2 |
Dans les stations météorologiques les relevés de vent sont effectués à une hauteur standard de 10 m au-dessus d’un terrain plat et découvert. La direction du vent est déterminée par une girouette, et sa vitesse par un anémomètre.
À ce jour, il n’existe pas de relation mathématique établie permettant de déterminer la vitesse et la direction du vent en un lieu et à un moment donnés. C’est ce qui explique la difficulté de prévoir le temps, même à moyen terme! Ceci étant, il est possible de déterminer qualitativement les variations locales du vent.
| Le vent en un lieu est dépendant du type d’environnement et des obstacles rencontrés. |
> En guise de conclusion
Les vents dominants en Belgique soufflent du sud-ouest, mais aux changements de saisons la fréquence du vent est tout aussi importante du nord-est. Il y a très peu de vent d’orientation nord-ouest ou sud-est.
Les vents du nord-est sont polaires, donc froids et secs, tandis que la direction sud-ouest est celle des alizés chauds. Lorsqu’ils proviennent plutôt du sud ils sont secs, tandis que de l’ouest ils amènent la pluie.
À l’exception de la région côtière, pendant plus de 60 % du temps, la vitesse du vent est inférieure à 20 km/h. Le long de la mer, la vitesse du vent est 70 % plus élevée que dans le reste du pays.
Influence de l’environnement sur le vent
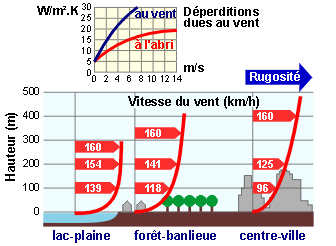
L’environnement a une grande influence sur la vitesse et la direction du vent.
Puisque celui-ci influence de façon importante le taux d’infiltration d’air du bâtiment et donc la détermination des besoins en énergie du bâtiment, il est essentiel de connaître l’environnement dans lequel le bâtiment va être construit.
La figure ci-dessus donne les variations de la vitesse du vent selon l’altitude et la nature du sol
- Calcul du facteur de pond. à appliquer sur le taux d’infiltration en fonction de l’environnement dans lequel on se trouve
- Analyse des paramètres agissant sur le vent et sa vitesse
Calcul du facteur de pondération à appliquer sur le taux d’infiltration en fonction de l’environnement dans lequel on se trouve (méthode utilisée dans Opti)
On distingue 4 classes :
| > | classe 1 : | bord de mer (–> 2 km de la digue). |
| > | classe 2 : | zone rurale avec bâtiments ou arbres isolés. |
| > | classe 3 : | zone urbanisée, industrielle ou forestière. |
| > | classe 4 : | ville (zone de construction d’au moins 10 m de haut sur au moins le quart de la surface). |
–> norme NBN B03-002 “actions du vent sur les constructions”
Pour calculer la vitesse du vent à une hauteur bien précise, il faut appliquer la formule
V = Vref λ ln (Z/Zo)
où,
- Vref = vitesse à une hauteur de 10 m
- Z = hauteur pour laquelle la vitesse est recherchée
- λ et Zo ont des valeurs différentes en fonction de la classe de la zone.
| Classe | λ | Zo |
|
1 2 3 4 |
0.166 0.202 0.234 0.209 |
0.005 0.07 0.30 1 |
Or, la vitesse en hiver à Uccle est de 4.7 m/sec à 10 m de hauteur et la hauteur moyenne d’une habitation individuelle = 5 m.
Donc la vitesse du vent à une hauteur de 5 m est de
- dans une zone de classe 2 :
V = 4.7 x 0.202 ln (5/0,07) = 4.05 m/sec
- dans une zone de classe 1 :
V = 4.7 x 0.166 ln (5/0,005) = 5.389 m/sec
- dans une zone de classe 3 :
V = 4.7 x 0.234 ln (5/0,3) = 3.09 m/sec
- dans une zone de classe 4 :
V = 4.7 x 0.209 ln 5/1 = 1.58 m/sec
Dans les recherches effectuées par l’AIVC, on retrouve des graphes donnant, en fonction du degré d’étanchéité de l’habitation, le taux d’infiltration en fonction de la vitesse du vent.
Pour une hauteur moyenne de 5 m (c’est-à-dire pour une habitation individuelle)
|
en zone II, si pour |
V = 4.05m/sec, | τ = 0.30 vol/h | |
| alors | en zone I, | V = 5.39m/sec, | τ = 0.35 vol/h |
| – | en zone III, | V = 3.09m/sec, | τ = 0.25 vol/h |
| – | en zone IV, | V = 1.58m/sec, | τ = 0.2 vol/h |
|
en zone II, si pour |
V = 4.05m/sec, | τ= 0.45 vol/h | |
| alors | en zone I, | V = 5.39m/sec, | τ = 0.55 vol/h |
| – | en zone III, | V = 3.09m/sec, | τ = 0.40 vol/h |
| – | en zone IV, | V = 1.58m/sec, | τ = 0.35 vol/h |
|
en zone II, si pour |
V = 4.05m/sec, | τ = 0.95 vol/h | |
| alors | en zone I, | V = 5.39m/sec, | τ = 1.1 vol/h |
| – | en zone III, | V = 3.09m/sec, | τ = 0.80 vol/h |
| – | en zone IV, | V = 1.58m/sec, | τ = 0.65 vol/h |
Donc, le facteur de pondération à appliquer sur le taux d’infiltration en fonction de la classe de la zone sera :
> Si maison étanche, c’est-à-dire tinf < 0.4 vol/h
classe 1 : INF = INF x (0.35/0.30)
classe 2 : INF = INF
classe 3 : INF = INF x (0.25/0.3)
classe 4 : INF = INF x (0.2/0.3)
> Si maison moyennement étanche, c’est-B-dire 0.4 < tinf < 0.8 vol/h
classe 1 : INF = INF x (0.55/0.45)
classe 2 : INF = INF
classe 3 : INF = INF x (0.4/0.45)
classe 4 : INF = INF x (0.35/0.45)
> Si maison non étanche, c’est-à-dire tinf > 0.8 vol/h
classe 1 : INF = INF x (1.1 /0.95)
classe 2 : INF = INF
classe 3 : INF = INF x (0.8/0.95)
classe 4 : INF = INF x (0.65/0.95)
Analyse des paramètres agissant sur le vent et sa vitesse
Les gradients de température principalement créés par l’ensoleillement sont responsables des mouvements d’air. Ils engendrent l’ascension de masses d’air chaud et un appel d’air froid. Divers types d’environnement sont propices à ces phénomènes :
|
Les étendues d’eau
Les masses d’eau étant plus chaudes que l’atmosphère en hiver et plus fraîches en été, les courants d’air créés par le gradient thermique s’inversent au cours de l’année. Lors des brusques variations de température (nuits fraîches par exemple) les courants d’air peuvent aussi s’inverser au cours d’une même journée.
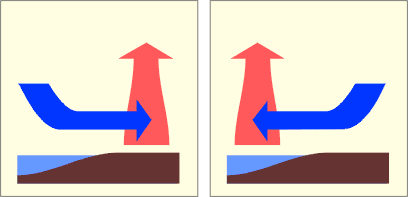
Les versants de collines
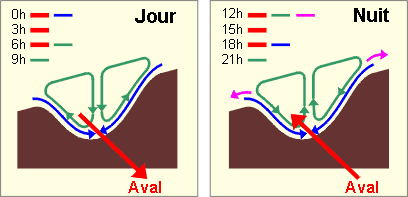
Sur les versants de collines, le soleil favorise un gradient de température et donc des courants d’air durant la journée. De nuit, le gradient s’estompe et puis s’inverse légèrement, de telle sorte que l’air circule dans le sens opposé.
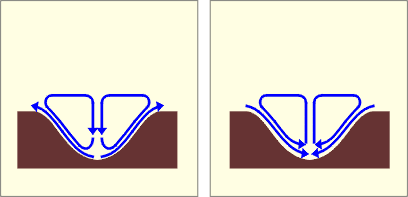
Les longues vallées
Dans les longues vallées, le phénomène expliqué ci-dessus tend à créer un mouvement d’air longitudinal d’autant plus puissant que la vallée est longue et que le gradient de température est élevé. Le dessin ci-contre illustre la complexité des mouvements d’air.
Les villes
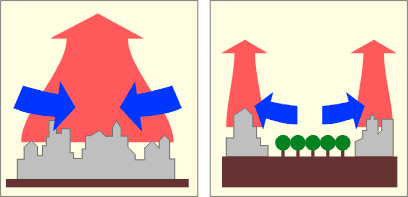
La température des villes étant supérieure à celle des campagnes, on y constate un mouvement d’air similaire à celui créé par les masses d’eau. L’appel d’air se dirige vers les villes. De même, en ville, les grands espaces dégagés permettent la création de courants d’air.
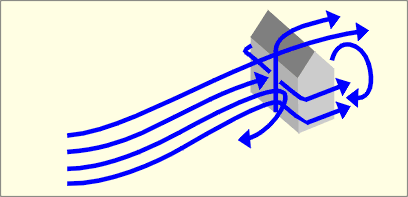
Les obstacles constituent diverses obstructions et provoquent des modifications de la vitesse et de la direction du vent. Lorsque le vent rencontre un mur, par exemple, il est obligé de le contourner. La face d’un objet exposée au vent subit une surpression tandis que la face opposée est soumise à une dépression.

De manière générale, le vent étant freiné par les obstacles, lorsque la densité et la taille de ceux-ci sont importants (en ville par exemple), la vitesse du vent est moindre qu’en sites dégagés tels que les champs et les étendues d’eau.
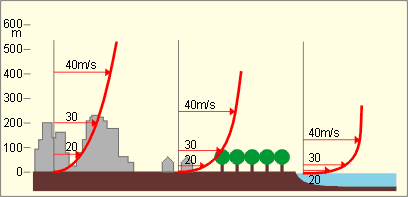
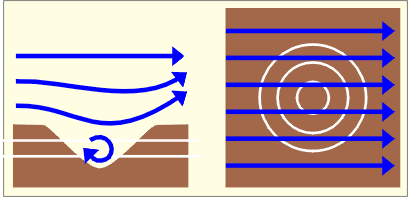
La topographie
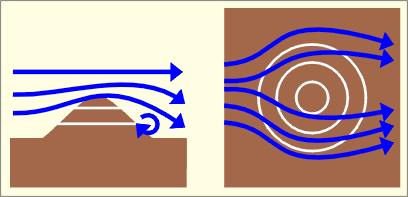
La topographie ne constitue pas à proprement parler un obstacle mais elle engendre éventuellement des modifications par rapport aux données générales relatives au vent.
Ces changements s’effectuent à moyenne ou grande échelle. Le relief a pour effet de protéger certains sites mais aussi d’en surexposer d’autres. Par ailleurs, il peut modifier les vents dominants sur des grandes étendues. Ci-contre, deux schémas illustrent le flux de vent rencontrant une colline et une dépression.
Les obstacles au vent peuvent prendre des formes très variées : les constructions forment des écrans permanents tandis que la végétation peut présenter de nombreuses variations de taille (croissance) et d’opacité (saisons).
Certains de ces écrans amovibles ou non peuvent également être utilisés à volonté afin de protéger les espaces extérieurs.
Outre la protection qu’ils offrent, la proximité d’écrans peut occasionner des effets secondaires tels que courants d’air et turbulences.
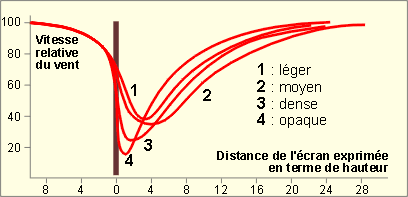
L’efficacité d’un écran est régie par ses dimensions et sa perméabilité.
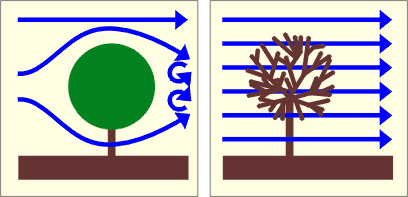
La perméabilité de l’écran importe également. Ainsi, les écrans denses provoquent une forte réduction de la vitesse du vent sur une faible profondeur tandis que les écrans perméables réduisent la vitesse du vent dans une moindre mesure mais sur une profondeur plus importante.
La profondeur de la zone protégée est proportionnelle à la hauteur de l’écran : sa taille sera maximale lorsque l’écran aura une longueur équivalente à 11 à 12 fois sa hauteur.
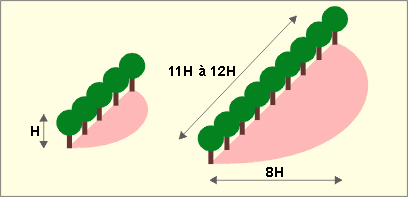
Les plantations à feuilles caduques offrent une meilleure protection estivale qu’hivernale. Leur effet est négligeable durant l’hiver.
Source – Logiciel OPTI Bureaux – Architecture et Climat – juin 2000





Auteur : les anciens
Notes :