Sommaire
Attention : tous les coûts indiqués dans ce fichier sont basés sur un prix du litre de fuel à 0,622 €.
Le coût d’un m³ traité en hiver
L’énergie nécessaire pour traiter (= chauffer et humidifier) un m³ d’air, est donnée par la différence d’enthalpie (= d’énergie) entre l’air extérieur “E” et l’air soufflé dans le local “S”.
Δ h = hS – hE [kJ/kg]
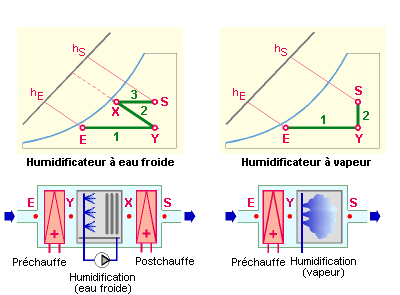
Les enthalpies de ces deux états de l’air sont indiqués dans le diagramme de l’air humide (il est également possible de réaliser le calcul de l’enthalpie à partir de la valeur de la température et de l’humidité relative).
Les valeurs des enthalpies sont exprimées kilo joule par kg. Pour obtenir la valeur exprimée en m³, il faudra multiplier celle-ci par la masse volumique ρ de l’air.
Question : quelle masse volumique prendre ? celle de l’air extérieur (froid et contracté) ou celle de l’air soufflé (chaud et dilaté) ? Pour éviter ce problème, les bureaux d’étude travaillent toujours avec les masses d’air (constantes) et non les volumes! La conversion vers les m³ ne se fait qu’au moment de dimensionner le ventilateur. Celui-ci étant souvent positionné à la sortie de caisson de traitement d’air, on prendra la masse volumique de l’air soufflé.
Le coût final du traitement de l’air est alors fonction du type d’énergie utilisé. Dans l’exemple ci-dessous (conditions moyennes), le coût du traitement de 1 000 m³/h varie entre 72,5 et 105,5 c€/heure.
| Exemple.
Soit :
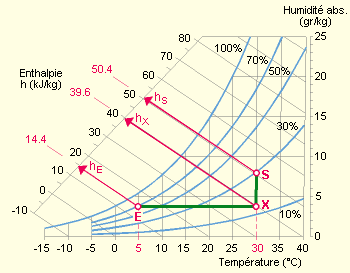
Quelle est l’énergie nécessaire pour chauffer 1 000 m³/h ? Δ h = hS – hE = 50,4 – 14,4 = 36 [kJ/kg] Sachant que l’air soufflé présente une masse volumique de 1,15 kg/m³ : Δ h = 36 [kJ/kg] x 1,15 [kg/m³] = 41,4 [kJ/m³] Si le débit d’air pulsé est de 1 000 m³/h, l’énergie à fournir par heure : 1 000 [m³/h] x 41,4 [kJ/m³] = 41 400 [kJ/h] = 41,4 [MJ/h] Pour déterminer le coût de ce traitement, il faut distinguer selon le mode d’humidification : Si l’humidification est réalisée par un humidificateur à eau froide (humidificateur à évaporation ou à pulvérisation), la chaleur de vaporisation de l’eau est donnée par le système de chauffage de l’air. En prenant un coût moyen de l’énergie thermique de 1,75 c€ le MJ (6,22 c€ le kWh), on obtient un coût horaire de : 41,4 [MJ/h] x 1,75 [c€/MJ] = 72,5 [c€/h] Si l’humidification est réalisée par un humidificateur à vapeur autonome (alimentation électrique), il faudra dissocier l’énergie thermique nécessaire pour le chauffage de l’air, de l’énergie électrique nécessaire pour l’humidification. Le point intermédiaire “X” à la sortie de la batterie de chauffe et à l’entrée de l’humidificateur est situé (en bonne approximation) à l’horizontale de l’air extérieur E et sur la verticale de la température 30°C.
Le diagramme de l’air humide fournit un point de caractéristique X : 30° 15 % HR, enthalpie 39,6 kJ/kg. En prenant un coût moyen de l’énergie thermique de 1,75 c€ le MégaJoule (6,22 c€ le kWh) et un coût moyen de l’énergie électrique de 4,45 c€ le MégaJoule (16 c€ le kWh, en tenant compte du coût de la pointe de puissance), on obtient : Chauffage de l’air (de 5°C 70 % HR à 30°C 15 % HR) : 1 000 [m³/h] x 1,15 [kg/m³] x (39,6 – 14,4) [kJ/kg] x 0,001 [MJ/kJ] x 1,75 [c€/MJ] = 50 [c€/h] Humidification de l’air (de 30°C 15 % HR à 30°C 30 % HR) : 1 000 [m³/h] x 1,15 [kg/m³] x (50,4 – 39,6) [kJ/kg] x 0,001 [MJ/kJ] x 4,45 [c€/MJ] = 55,5 [c€/h] Soit un total de 105,5 c€/h. |
Le coût d’un m³ traité en été
L’énergie nécessaire pour traiter (= refroidir et déshumidifier) un m³ d’air est en principe donnée par la différence d’enthalpie (= d’énergie) entre l’air extérieur E et l’air soufflé S.
Δ h = hE – hS [kJ/kg]
Toutefois, il se peut que le traitement de l’air en été suppose un refroidissement (avec déshumidification) suivi d’un post-chauffage. Dans ce cas, si X est le point caractéristique de l’air à la sortie de la batterie de refroidissement, on aura :
Δ h = énergie frigorifique + énergie calorifique = (hE – hX) + (hS – hX) [kJ/kg]
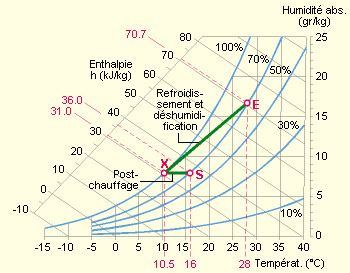
Les enthalpies de ces deux états de l’air sont indiqués dans le diagramme de l’air humide (il est également possible de réaliser le calcul de l’enthalpie à partir de la valeur de la température et de l’humidité relative).
Les valeurs des enthalpies sont exprimées par kg. Pour obtenir la valeur exprimée en m³, il faudra multiplier celle-ci par la masse volumique ρ de l’air.
Question : quelle masse volumique prendre ? celle de l’air extérieur (chaud et dilaté) ou celle de l’air soufflé (froid et contracté) ? Pour éviter ce problème, les bureaux d’étude travaillent toujours avec les masses d’air (constantes) et non les volumes ! La conversion vers les m³ ne se fait qu’au moment de dimensionner le ventilateur. Celui-ci étant souvent positionné à la sortie de caisson de traitement d’air, on prendra la masse volumique de l’air soufflé.
Le coût final du traitement de l’air est alors fonction du prix de l’énergie utilisée. Dans l’exemple ci-dessous (conditions moyennes), le coût du traitement de 1 000 m³/h est estimé à 99,5 c€/heure.
| Exemple.
Soit,
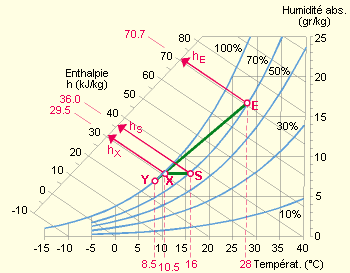
Quelle est l’énergie nécessaire pour refroidir 1 000 m³/h ? Imaginons un refroidissement et une déshumidification par passage dans une batterie froide alimentée au régime 6°C – 11°C (soit une température moyenne de 8,5°C). Le point caractéristique de l’air “X” en sortie de batterie sera situé à l’intersection entre la droite qui relie le point E au point Y (Y = 8,5°C et 100 % HR) et l’horizontale du point S. Le point X a pour caractéristiques : 10,5°C et 97 % HR, hX = 31 kJ/kg.
On en déduit une énergie frigorifique : Δ h = hE – hX = 70,7 – 31 = 39,7 kJ/kg Mais pulser un air de 10,5°C dans un local entraînerait un risque d’inconfort ! Aussi, on le préchauffera jusqu’à 16°C, entraînant une énergie de chauffage de : Δ h = hS– hX = 36 – 31 = 5 kJ/kg Soit un total de 41,2 + 5 = 46,2 kJ/kg Sachant que l’air soufflé présente une masse volumique de 1,20 kg/m³ : Δ h = 46,2 kJ/kg x 1,20 kg/m3 = 55,4 kJ/m³ Si le débit d’air pulsé est de 1 000 m³/h, l’énergie à fournir par heure : 1 000 m³/h x 55,4 kJ/m3 = 55 400 kJ/h = 55,4 MJ/h On constate qu’il y a “destruction de l’énergie”, c’est-à-dire qu’il faut compter deux fois la différence d’enthalpie entre X et S : une fois pour le refroidissement et une deuxième fois suite au post-chauffage. Ceci est cependant obligatoire si l’on souhaite atteindre un tel niveau de déshumidification… Pour déterminer le coût de ce traitement, il faut déterminer le prix de revient du kWh frigorifique. Supposons l’utilisation d’une machine frigorifique dont le COPfroid moyen réel (ou efficacité frigorifique) est de 2,5. Il faut donc 1 kWh électrique au compresseur pour extraire un 2,5 kWh thermique à l’évaporateur. S’il s’agit du courant électrique de jour (prix de revient moyen +/- 16 c€/kWh, pointe 1/4 horaire comprise), il en coûtera donc 6,4 c€ par kWh thermique extrait. Soit 1,8 c€/MJ. Pour la partie chauffage, un coût moyen de l’énergie thermique de 1,75 c€ le MégaJoule (6,22 c€ le kWh) est proposé. Le coût total devient donc : 1 000 [m³/h] x 1,20 [kg/m³] x (41,2 [kJ/kg] x 1,8 [c€/MJ] + 5 [kJ/kg] x 1,75 [c€/MJ]) x 0,001 [MJ/kJ] = 99,5 [c€/h] |
Le coût de l’humidification
L’humidité de l’air constitue une bonne part de son énergie !
Par exemple, de l’air sec à 20°C possède une enthalpie (= énergie) de 20,1 kJ/kg. Mais le même air, humidifié à 50 % d’humidité relative, atteindra 38,5 kJ/kg. Cela s’explique par le fait que l’humidité est constituée par de l’eau à l’état vapeur et que la chaleur de vaporisation de l’eau est proportionnellement très élevée.
Le graphe ci-dessous montre l’évolution de l’enthalpie de l’air en fonction de son humidité relative.
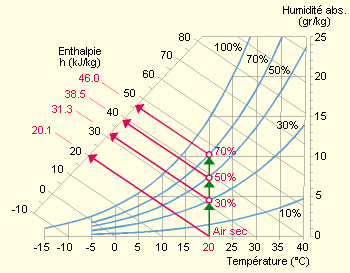
L’humidification de l’air est donc fort énergétique. On aura donc toujours intérêt à diminuer la consigne du taux d’humidité relative en hiver (40 % HR, par exemple).
Mais, en hiver, il faut toujours humidifier l’air de chauffage…
En hiver, l’humidité absolue de l’air extérieur est toujours très faible. Imaginons qu’il vient de pleuvoir, que l’air extérieur est proche de la saturation (100 % HR). Pour une température extérieure de + 1°C, cela ne représente jamais qu’une humidité absolue de 4 grammes d’eau par kg d’air. Or, de l’air à 20°C et 50 % HR contient 7,5 grammes d’eau par kg d’air. Il faudra donc humidifier l’air extérieur après son chauffage et avant de le pulser dans le local.
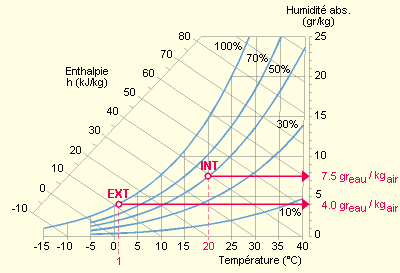
Dans l’exemple ci-dessous, on montre que le passage de la consigne de 20°C 50 % HR à 20°C 60 % HR entraîne une augmentation des coûts de 6 à 11 %, alors que l’occupant ne percevra aucune différence en terme de confort.
| Exemple.
Reprenons l’exemple développé pour le calcul du coût d’1 m³ traité en hiver. Les conditions de calcul étaient les suivantes : soit,
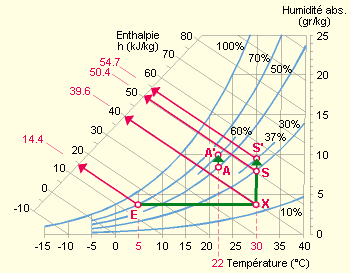
Un tel point de soufflage correspond généralement à un immeuble de bureaux dans lequel on veut maintenir une ambiance “A” de 22°C et 50 % HR (l’humidité absolue de l’air soufflé est légèrement plus faible que l’ambiance, ce qui permet de compenser les apports en eau des occupants). L’énergie demandée par le traitement de 10 000 m³/h est de Chauffage de l’air (de 5°C 70 % HR à 30°C 15 % HR) : 1 000 m³/h x 1,15 kg/m³ x (39,6 – 14,4) kJ/kg x 0,001 MJ/kJ = 29 MJ/h Humidification de l’air (de 30°C 15 % HR à 30°C 30 % HR) : 1 000 m³/h x 1,15 kg/m³ x (50,4 – 39,6) kJ/kg x 0,001 MJ/kJ = 12,4 MJ/h
Supposons que la consigne soit modifiée et que A’ (22°C et 60 % HR) soit demandé. On pulsera probablement un air de chauffage de 30°C et 37 % HR. L’enthalpie de ce nouveau point S’ est de 54,7 kJ/kg. Soit un nouveau calcul pour l’humidification de l’air. 1 000 m³/h x 1,15 kg/³ x (54,7 – 39,6) kJ/kg x 0,001 MJ/kJ = 15,1 MJ/h Le bilan énergétique total est donc augmenté de 6,5 % pour une amélioration du confort imperceptible au niveau des occupants. Le coût total du traitement de l’air est augmenté de 6,5 % si l’eau est froide dans l’humidificateur (chaleur de vaporisation prise sur l’air) et de 11 % si l’humidification est réalisée par un humidificateur électrique à vapeur. |

Auteur : les anciens
Mars 2009 : Thibaud
Notes :