Sommaire

La perméance thermique d’une couche de matériau
La perméance thermique (P) indique la quantité de chaleur qui se propage :
- en 1 seconde,
- à travers 1 m² d’une couche de matériau,
- d’une épaisseur déterminée,
- lorsque la différence de température entre les deux faces est de 1 K (1 K = 1 °C).
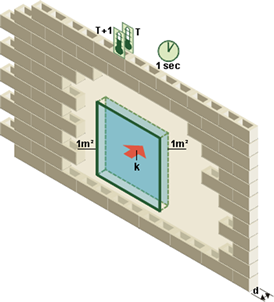
> La perméance thermique s’exprime en W/m²K.
Plus la perméance thermique est élevée, plus la couche laisse passer la chaleur.
Ce coefficient est valable aussi bien pour les matériaux homogènes que pour les matériaux non-homogènes.
- Matériau homogène : P = λ / d où d = épaisseur de la paroi.
- Matériau non-homogènes : P est déduite d’essais effectués en laboratoire.
La résistance thermique d’une couche de matériau
La notion de perméance thermique est peu utilisée. Elle permet d’introduire et de mieux comprendre la résistance thermique (R) qui est l’inverse de la perméance thermique.
R = 1 / P
> Elle s’exprime en m²K/W.
C’est la mesure de performance isolante de la couche de matériau. Plus la résistance thermique est élevée, plus la couche est isolante.
Ce coefficient est valable aussi bien pour les matériaux homogènes que pour les matériaux non homogènes.
Matériau homogène
La résistance thermique est obtenue par le rapport entre l’épaisseur (en m) et la conductivité thermique de la couche du matériau (en W/m.K) :
R = d / λ
Matériau non-homogène
La résistance thermique utile Ru est déduite d’essais effectués en laboratoire.
La valeur déclarée
La valeur déclarée RD d’une couche de matériau de construction est généralement fournie par son fabricant. Cette valeur est certifiée sur base d’un agrément technique (ATG, CE, ETA, ETZ, …). Elle est obtenue dans des conditions de référence données de température et d’humidité (d’après les principes donnés dans la EN ISO 10456).
Les valeurs de calcul
À partir de cette valeur RD, il est possible de déduire les valeurs de calcul de la conductivité thermique RU,i et RU,e qui correspondent aux conditions d’utilisation du matériau (interne ou externe).
Il existe un site officiel (![]() www.epbd.be) qui indique, pour les trois régions belges, les valeurs RU,i et RU,e de certains matériaux qui peuvent être utilisées pour le calcul des performances thermiques des parois suivant la réglementation PEB.
www.epbd.be) qui indique, pour les trois régions belges, les valeurs RU,i et RU,e de certains matériaux qui peuvent être utilisées pour le calcul des performances thermiques des parois suivant la réglementation PEB.
Les valeurs de calcul par défaut
Des valeurs de calcul RU,i par défaut peuvent toujours être utilisées lorsque le matériau ne possède pas de valeur RD certifiée ou n’est connu que par sa nature. Ces valeurs sont reprises dans un tableau de la réglementation.
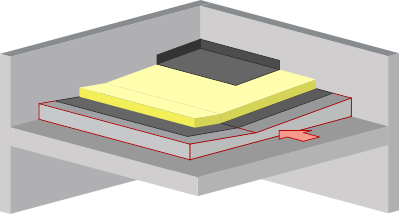
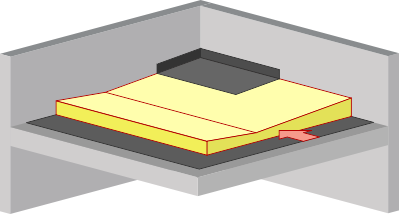
La résistance thermique d’une couche de matériau homogène d’épaisseur variable
Dans les parois de l’enveloppe du volume protégé, certaines couches peuvent avoir des épaisseurs variables.
Exemples :
|
Un béton de pente
Une couche d’isolant à épaisseur variable |
Méthode simplifiée
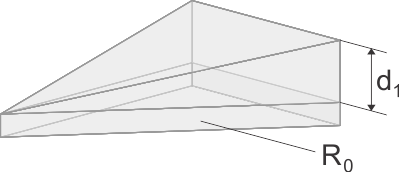
La résistance thermique de cette couche peut être déterminée de manière sécuritaire en considérant que son épaisseur est partout égale à son épaisseur la plus faible dmin -> R = dmin/λ.
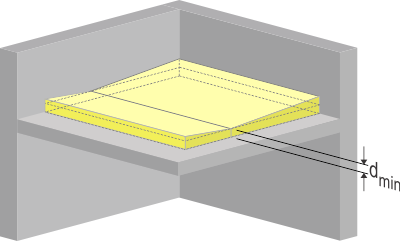
Épaisseur dmin
Méthode précise
Si la différence de pente entre les deux faces de la couche est inférieure à 5 %, une méthode de calcul existe pour quantifier avec plus de précision les performances thermiques de la paroi. Celle-ci est décrite dans l’Annexe B1 de l’AGW du 15 mai 2014 à l’Art. 7.4.
Elle consiste à décomposer la paroi en éléments partiels de formes déterminées et à calculer à l’aide de formules directement la valeur U de chacun de ces éléments.
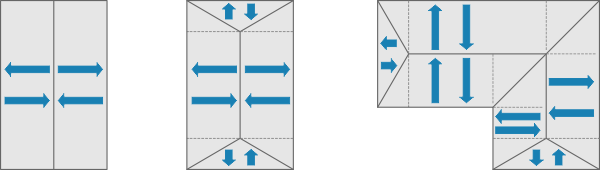
Décomposition de la paroi en éléments partiels.
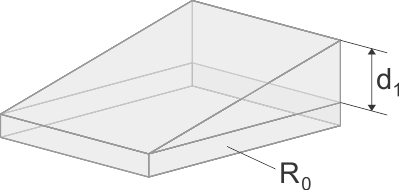
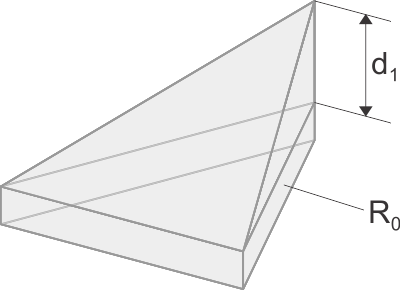
Les formes de base :
| Rectangulaire
U = 1/R1 . ln [1 + R1/R0] Triangulaire avec partie la plus épaisse à la pointe
U = 2/R1 . [(1 + R0/R1) . ln (1+R1/R0) – 1] Triangulaire avec partie la plus mince à la pointe
U = 2/R1 . [1 – R0/R1 . ln (1+R1/R0)] Avec :
|
Un outils de calcul développé par l’IBGE existe et est disponible ici. XLS
Si par contre, la différence de pente entre les deux faces de la couche est supérieure à 5%, cette méthode ne s’applique pas et un calcul numérique doit être réalisé.
La résistance thermique d’une couche de mousse de polyuréthane (PUR) projetée in situ
Il est difficile d’évaluer l’épaisseur exacte d’une couche de mousse de polyuréthane projetée in situ.

PUR projeté.
C’est la raison pour laquelle la résistance thermique R de cette couche est multipliée par un terme correctif a qui varie en fonction du type d’application.
R PUR projeté = a x R PUR en plaque
- a vaut 0.85 pour les applications en toiture.
- a vaut 0.925 pour les applications sur sol.
Source: AGW du 15 mai 2014, Annexe B1, Art 7. 3

PUR projeté en toiture.

PUR projeté sur sol.
La résistance thermique d’une couche de maçonnerie
Une maçonnerie est constitué de briques ou de blocs assemblés et solidarisés entre eux par du mortier. La résistance thermique d’une couche de maçonnerie devra donc prendre en compte l’épaisseur de ce joint de mortier.
Si cette épaisseur est inférieure à 3 mm, on peut considérer que les briques ou blocs sont collés. Dans ce cas, le coefficient de conductivité thermique utile λU de la maçonnerie est égal à celui des briques ou blocs. La résistance thermique de la couche est donc égale à l’épaisseur de la maçonnerie divisée par le coefficient de conductivité thermique de la brique ou du bloc.
R = dU,maç / λU,brique/bloc

Blocs collés.
Si cette épaisseur est supérieure à 3 mm, il faudra tenir compte de la présence des joints pour déterminer le coefficient de conductivité thermique λU moyen de la maçonnerie.
λU,moyen = (λU,brique/bloc x Surface brique/bloc + λU,joint x Surface joint) / Surface totale
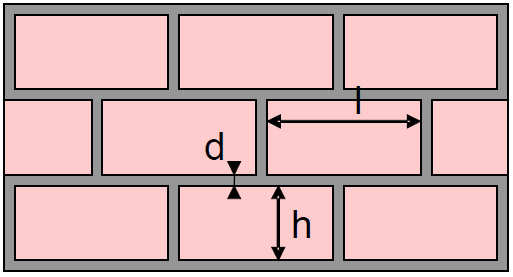
- Surfacejoint = (l + h + d) x d
- Surfacebrique/bloc = l x h
- Surfacetotale = (l + d) x (h + d)
La résistance thermique de la couche est donc égale à l’épaisseur de la maçonnerie divisée par le coefficient de conductivité thermique moyen.
R = dmaç / λU,moyen
Valeurs par défaut
Lorsque la proportion de joints n’est pas connue,
- si la conductivité thermique des joints est inférieure à des biques ou blocs, on peut considérer la maçonnerie comme collée (donc sans joints) ;
- si la conductivité thermique des joints est supérieure à des biques ou blocs, on peut considérer :
- la fraction joints égale à 16 % pour les maçonneries intérieures et
- la fraction joints égale à 28 % pour les maçonneries extérieures.
Source: AGW du 15 mai 2014, Annexe B1, Art. G.3.1
La résistance thermique d’une couche non homogène d’un élément de construction avec structure bois
Les parois du volume protégé peuvent contenir des couches de matériaux non-homogènes dans lesquelles une structure bois est incorporée et dont le reste de l’espace est occupé par un matériau isolant.
Exemples :
- chevrons d’une toiture inclinée ;
- gîtage d’une toiture plate, d’un plafond ou d’un plancher en bois;
- structure d’une façade légère à ossature bois ;
- …

Façades et plancher à ossature bois.

Toit incliné à chevrons.
Cette structure affaiblit le pouvoir isolant de la couche. Il faut donc en tenir compte pour en calculer la résistance thermique.
Celle-ci dépend de la fraction bois. Dans le cas d’une structure régulière, la fraction bois est égale à la largeur des éléments en bois divisée par la distance moyenne entre les éléments (d’axe en axe).
|
|
% bois = d / l moyen |
Cette fraction est généralement augmentée de 1 % pour tenir compte des entretoises.
Calcul de la résistance thermique de la couche
La résistance thermique de la couche se calcule donc en utilisant un coefficient de conductivité thermique λU moyen.
λU,moyen = λU,bois x % bois + λU,isolant x (100 % – % bois)
La résistance thermique de la couche est donc égale à l’épaisseur de la couche divisée par le coefficient de conductivité thermique moyen.
R = d / λU,moyen
Valeurs par défaut
La réglementation propose l’utilisation de valeurs par défaut. Elles correspondent aux limites supérieures des valeurs les plus courantes en fonction du type de paroi. Celles-ci sont reprises dans le tableau suivant :
| Structure en bois | Fraction de bois (valeur par défaut) |
|---|---|
| Toiture à pannes (pannes-structure portante primaire) |
0,11 |
| Toiture à pannes (chevrons-structure portante secondaire) |
0,20 |
| Toiture à fermes (fermettes-structure portante secondaire) |
0,12 |
| Planchers en bois (poutres-structure portante secondaire) |
0,11 |
| Parois à ossature en bois | 0,15 |
Source: AGW du 15 mai 2014, Annexe B1, Art G.4






Date :
Auteur :
Notes :
Source :
[…] Par contre, si la demande était à nouveau introduite via le programme UREBA actualisé (depuis octobre 2022) qui stipule que le coefficient de résistance thermique R de l’isolant ajouté sera supérieur ou égal 6 ; les 20 cm de laine minérale ne suffisent plus car la résistance thermique affichée pour ces 20 cm est de 5,70. Pour satisfaire cette exigence renforcée, il faudra pour un même matériau viser une épaisseur plus grande (22 cm minimum) ou une valeur U inférieure à 0,035. > La résistance thermique d’une couche de matériau […]